(R/I)-Modules .... Dummit and Foote Example (5), Section 10.1

[Math Amateur]

I am reading Dummit and Foote's book: "Abstract Algebra" (Third Edition) ...

I am currently studying Chapter 10: Introduction to Module Theory ... ...

I need some help with an aspect of Example (5) of Section 10.1 Basic Definitions and Examples ... ...

Example (5) reads as follows:

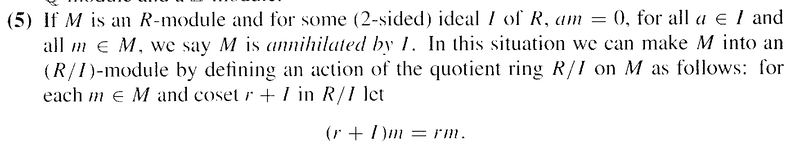
I do not fully understand this example and hence need someone to demonstrate (explicitly and completely) why it is necessary for $am = 0$ for all $a \in I$ and all $m \in M$ for us to be able to make $M$ into an $(R/I)$-module. ...
Help will be much appreciated ..

Peter

 

[member 587159]

Hey Peter.

It is needed to make sure that the operation that turns $M$ in a $R/I$ module is well defined, i.e., one must show that what is written down, is a (well-defined) function.

This is routine work.

Indeed, suppose that $(r_1 + I, m_1) = (r_2 +I,m_2)$, then $m_1 = m_2$ and $r_1 + I = r_2 + I$.

The latter one implies that $r_1 - r_2 \in I$, and by assumption $m_1(r_1 - r_2) = 0$, so that $m_1r_1 = m_1r_2 = m_2r_2$ and hence the function is well defined.

Hope this helps.

 

[Math Amateur]

Thanks Math_QED ...

BUT ... I need a clarification ...

Dummit and Foote write elements of the $R/I$-module as $m$ ... what are the elements of the form $(m_1, r_1 + I)$?

I can understand an element of the form $(r+I)m$ belongs to the left $R/I$-module ... but how do we get an element of the form $(m_1, r_1 + I)$?

Can you help ...

Sorry if i am being slow ...

Peter***EDIT***

Did you mean $(m_1, r_1 + I) \equiv m_1(r_1 + I)$ ... that is an element from a right $R/I$-module ...?

 

[member 587159]

Thanks Math_QED ...

BUT ... I need a clarification ...

Dummit and Foote write elements of the $R/I$-module as $m$ ... what are the elements of the form $(m_1, r_1 + I)$?

I can understand an element of the form $(r+I)m$ belongs to the left $R/I$-module ... but how do we get an element of the form $(m_1, r_1 + I)$?

Can you help ...

Sorry if i am being slow ...

Peter

Sorry, I wrote the module as a right module, while the book writes it as a left module. (I edited my previous post and changed the order in the tupels) However, this doesn't change your question of course. The operation in the R/I module M is:

$R/I \times M \to M: (r+I,m) \mapsto rm$

And for convenience we write this as $(r+I)m = rm$

But who says that what I wrote down is a function? This needs to be checked. I.e., one must check that for every element $(r+I,m) \in R/I \times M$, there is precisely one output associated with this input (see uniqueness of image in the definition of function).

That's what I proved: Hope it is clear now.

If you like an analogy that you have already encountered (probably), think about the function $\phi: G/\ker f \to f(G): g + \ker f \mapsto f(g)$ which you already encountered in the first isomorphism theorem of groups. We must also prove that this function is well defined.

 

[Math Amateur]

Thanks Math_QED ...

Yes ... clear now ... post above is most helpful ...

Peter

 

[Math Amateur]

Hi Math_QED ...

Another question that you may be able to help with ... I am puzzled about the definition and nature of the "multiplications" involved in the equation

$(r+I)m = rm$ ... ... ... ... ... (1)It seems to me that there are two multiplications involved and I am not sure how they are defined ... indeed suppose the two multiplications are $\star$ and $\circ$ ... ... then, (1) becomes$(r+I) \star m = r \circ m$But how are $\star$ and $\circ$ defined ... where do they come from ... what is their nature ,,,Can you help ... ...

 

[member 587159]

Hi Math_QED ...

Another question that you may be able to help with ... I am puzzled about the definition and nature of the "multiplications" involved in the equation

$(r+I)m = rm$ ... ... ... ... ... (1)It seems to me that there are two multiplications involved and I am not sure how they are defined ... indeed suppose the two multiplications are $\star$ and $\circ$ ... ... then, (1) becomes$(r+I) \star m = r \circ m$But how are $\star$ and $\circ$ defined ... where do they come from ... what is their nature ,,,Can you help ... ...

You are right: the multiplication in the R/I module is build using the multiplication in the R-module! This is something that is done a lot in mathematics: extending known structures to other structures.

This thing also happens for example when we define an operation on the sets of cosets $g+N$ where $g$ is an element of a group $G$ and $N$ is a normal subgroup. We define $(gN)\circ(hN) = (g.h)N$ where $\circ$ is the operation in the quotient group, $.$ the operation in the group $G$. This also gives another example of an addition where it is not clear whether this is well defined. Turns out that the addition I wrote down here makes sense if and only if $N$ is a normal subgroup.

To give a concrete answer to your question: the operation $\circ$ in your case is given. It is just an operation on the R-module $M$. The other one is defined, in terms of $\circ$, via the formula you wrote down.

 

[Math Amateur]

Thanks Math_QED ...

Very much appreciate all your help on the above issues ...

Peter