Freyster98
- 49
- 0
Homework Statement
Derive an expression geometrically for the radius of curvature of the following beam. This is part of a lab assignment for the bending of a simply supported beam with overhangs.
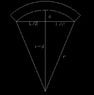
** I did this crappy diagram with AutoCAD, so I couldn't ( or didn't know how to ) include greek letters. Let's let r= \rho, and d= \delta for my derivation.
Homework Equations
a2+b2=c2
The Attempt at a Solution
I just used the pythagorean theorem to solve for \rho.
Starting with: \rho2= (\rho-\delta)2+(L/2)2.
Factoring out (\rho-\delta)2 , solving for \rho and simplifying , I end up with the following expression:
\rho=(\delta/2)+(L2/8\delta)I guess I have this question...is this the proper way to derive the radius of curvature geometrically? Is it ok to do it this way?
Attachments
Last edited: