Radius of insphere in a Tetrahedron

[Matejxx1]

Homework Statement

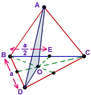
What is the largest possible radius of a sphere which is inscribed in a regular tetrahedron
a=10 ( this is the side of the tetrahedron)
r=?
r=5*√6/6

Homework Equations

The Attempt at a Solution

So first I calculated the Height of pyramid
a²=(2/3*v_a)²+h²
h=√(a²-(2/3*a*√3/2)²)
h=√(a²-(4*a²*3)/4)
h=√(a²-a²/3)
h=√(a²*2/3)
h=a*√(2/3)
and then I though since we have 2 similar triangles we could write the relation as
r/(h-r)=(2*v_a)/3a
r/(h-r)=2*a*√3/(3*a*2)
r/(h-r)=√3/3
r=(√3h-√3r)/3
3r=√3h-√3r
3r+√3r=√3*h
r(3+√3)=√3h
r=√3*h/(3+√3)
r=√3*a*√(2/3)/(3+√3)
r=a*√2/(3+√3)
r=a*√2+(3-√3)/(9-3)
r=(3a*√2-a√6)/6
r=2,99 which is wrong the right answer is
r=5*√6/6 but I don't know how to get it my only guess is that the relation is not correct but I don't know what else to try
any help would be really appreciated

 

[HallsofIvy]

I don't get either of those answers. I get that the radius of the largest sphere, that can be inscribed in a tetrahedron of edge length a, is a/4.

 

[Matejxx1]

Hey, Thanks for the answer!
I figured out how to do it with trial and error :P
By the way another question if I may.
I see most people posting equations like this

\frac{4s^3+4s^2+72}{s + 3}\;

Which is easier to read then (4s³+4s²+72)/(s+3)
mind telling me if you know how to do it ?

 

[LCKurtz]

Look here:
https://www.physicsforums.com/help/latexhelp/