No, I didn't notice. Can you show me?

[john baez]

A while ago I decided to figure out how to prove one of Ramanujan’s formulas. I feel this is the sort of thing every mathematician should try at least once.

I picked the easiest one I could find:

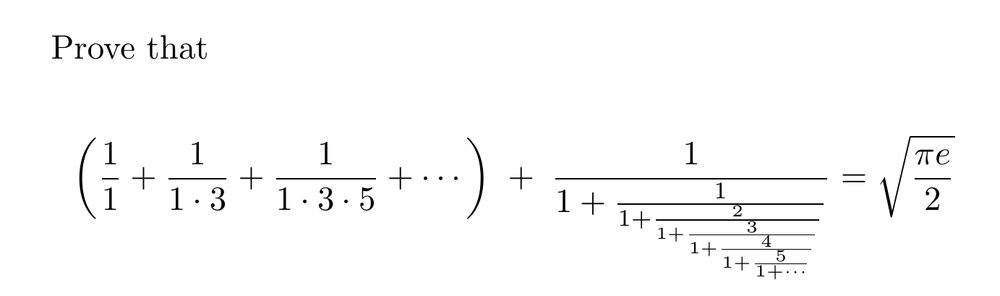
Hardy called it one of the “least impressive”. Still, it was pretty interesting: it turned out to be a puzzle within a puzzle! It has an easy outer layer which one can solve using standard ideas in calculus, and a tougher inner core which requires more cleverness - but still, nothing beyond calculus.

Read more and learn how to prove this formula here:

• Ramanujan's Easiest Formula.

 

[jedishrfu]

Interesting set of slides, I would not have thought to attack this problem using Taylor series and differential equations.

How did Ramanujan tackle it?

Was his approach limited to what he learned from the GS Carr book: A Synopsis of Elementary Results in Pure Mathematics?

It seems he could have approached it in the same way.

 

[john baez]

I would not have thought to attack this problem using Taylor series and differential equations.

When you see a series whose terms have something like factorials in their denominators:

$1 + \frac{1}{1 \cdot 3} + \frac{1}{1 \cdot 3 \cdot 5} + \cdots$

you should try to sum it using a Taylor series. A reasonable guess is to use this:

$f(x) = \frac{x}{1} + \frac{x^3}{1 \cdot 3} + \frac{x^5}{1 \cdot 3 \cdot 5} +\cdots$

You can try to just guess a function that has this Taylor series, but in this example it's rather hard, so it's better to play around by integrating $f$, differentiating it, multiplying it by stuff, and so on. The goal is to get equations you can solve to figure out what $f$ is.

How did Ramanujan tackle it?

I don't think anyone knows. But remember, he couldn't possibly have started by trying to prove this identity. He must have started by playing around with formulas and eventually found this identity.

Was his approach limited to what he learned from the GS Carr's book A Synopsis of Elementary Results in Pure Mathematics?

Quite possibly. Since Gaussians are so important he may have noticed that

$e^{x^2/2} \int_0^x e^{-t^2/2} \, dt = \frac{x}{1} + \frac{x^3}{1 \cdot 3} + \frac{x^5}{1 \cdot 3 \cdot 5} +\cdots$

and since he was a master of continued fractions, he probably also showed something like this:

$e^{x^2/2} \int_x^\infty e^{-t^2/2} \, d t = \frac{1}{x + \frac{1}{x + \frac{2}{x + \frac{3}{x + \frac{4}{\qquad {\ddots}}}}}}$

(A very similar formula is equation (1.8) in his first letter to Hardy, written in 1913.) It's easy to put these two formulas together and get

$\left(\frac{1}{1} + \frac{1}{1 \cdot 3} + \frac{1}{1 \cdot 3 \cdot 5} + \cdots\right) \; + \; \frac{1}{1 + \frac{1}{1 + \frac{2}{1 + \frac{3}{1 + \frac{4}{1 + \frac{5}{\quad{}_{\tiny{\ddots}}}}}}}} = \sqrt{\frac{\pi e}{2}}$

and this is the puzzle he posed in 1914.

 

[fresh_42]

This integration trick discloses how one of the problems I prepared for december can be solved. I wonder whether someone will notice.

 

[jedishrfu]

I didn't notice. Hey Mikey (@berkeman) did you notice?