Ratio of the area of triangles

[mathlearn]

View attachment 6006

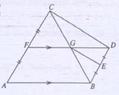
In the figure , the area of triangle $ABC$ is twice that of triangle $BCD$.USing the given information , find the ration of the area of the triangle $CFG$ to the area of triangle $BEG$

Hint- Use the midpoint theorem.

(Wave) Stuck in this problem & currently I have no workings to show.

 

[caffeinemachine]

In the figure , the area of triangle $ABC$ is twice that of triangle $BCD$.USing the given information , find the ration of the area of the triangle $CFG$ to the area of triangle $BEG$

Hint- Use the midpoint theorem.

(Wave) Stuck in this problem & currently I have no workings to show.

Note that $G$ is the mid-point of $BC$. Thus we have
$$[BEG]=(1/2)[BGD]=(1/4)[BCD]=(1/8)[ABC]=(1/2)[CFG]$$

 

[mathlearn]

Note that $G$ is the mid-point of $BC$. Thus we have
$$[BEG]=(1/2)[BGD]=(1/4)[BCD]=(1/8)[ABC]=(1/2)[CFG]$$

Many Thanks caffeinemachine (Happy)

Is the area of $\triangle CFG \frac{1}{2}$ the area of $\triangle CAB$?

 

[caffeinemachine]

Many Thanks caffeinemachine (Happy)

Is the area of $\triangle CFG \frac{1}{2}$ the area of $\triangle CAB$?

No. The area of $CFG$ is 1/4-th the area of $CAB$. This is easy to show. One way to show it is use the fact that $CFG$ and $CAB$ are similar triangles with corresponding side ratio's $1/2$.

 

[mathlearn]

No. The area of $CFG$ is 1/4-th the area of $CAB$. This is easy to show. One way to show it is use the fact that $CFG$ and $CAB$ are similar triangles with corresponding side ratio's $1/2$.

Thank you very much again (Sun)