Ray tracing in the movie Interstellar

[etotheipi]

https://arxiv.org/abs/1502.03808

They are using Boyer-Lindquist coordinates for the Kerr metric. As far as I understand they also introduced a camera-fixed basis defining spherical coordinates $\theta_{cs}$ and $\phi_{cs}$ to keep track of the directions of the light rays relative to the camera. Then from this they worked out the canonical momenta of the light rays and could finally solve numerically the following ray equations to figure out the source point $(\theta', \phi')$ of the rays on the celestial sphere:

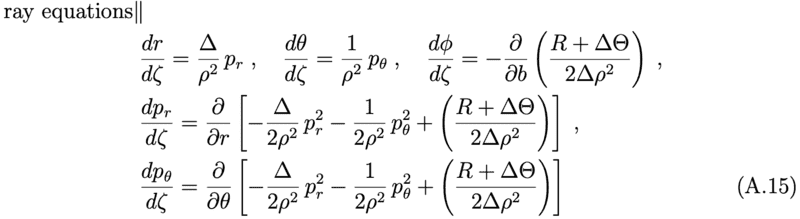
I would like to know how these equations are derived? There is a reference to Gravitation by Misner/Thorne/Wheeler but I don't have that and don't think I'd know where to look in any case!

 

[Ibix]

Not sure if this is exactly what you're looking for, but Kraniotis et al derive geodesic equations in Boyer-Linquist coordinates. I don't think they do the last step into a local frame, but that doesn't seem too hard if you have the camera worldline.

 

[etotheipi]

Not sure if this is exactly what you're looking for, but Kraniotis et al derive geodesic equations in Boyer-Linquist coordinates. I don't think they do the last step into a local frame, but that doesn't seem too hard if you have the camera worldline.

Gosh, that looks slightly scary! Thanks, okay I'll try and follow it. But I'm worried that I won't be able to get very far.

 

[Ibix]

Gosh, that looks slightly scary! Thanks, okay I'll try and follow it. But I'm worried that I won't be able to get very far.

I must say that I just implemented the equations in python...

 

[etotheipi]

I must say that I just implemented the equations in python...

Wait actually? That's sick! What for (if it's not confidential )?

 

[Ibix]

Fun, what else?

We did have a go at trying to work out the maximum time dilation you could get out of free-falling round a Kerr black hole. I used it for that - I think it was Steven Daryl who asked the question if you want to go looking for it.

 

[etotheipi]

I guess it's this one:
https://www.physicsforums.com/threa...me-travel-into-the-future.938858/post-5943810

That's really f*cking cool. Give me some time to go through all of this stuff and I'll shout later if I come up with questions

 

[etotheipi]

Hey Ibix I don't know if I'm being slightly stupid but I tried to run your thing and I got:

Trying escape trajectory - L=0.0
Trying escape trajectory - L=19.77811071962939
Found - beginning optimisation
Traceback (most recent call last):
File "kerr.py", line 189, in <module>
optimiseLaunches(KerrEquatorialSpacetime(1,0.99),4)
File "kerr.py", line 176, in optimiseLaunches
optimiseLaunch(st,E,Lcra,Lesc,"Best_"+str(E)+"_Max_")
File "kerr.py", line 143, in optimiseLaunch
orbitData=st.orbit(TIMELIKE,INWARD,E,Ltry,10*RM,15*RM,0.001,1000)
NameError: name 'RM' is not defined

 

[Ibix]

Somewhere between the st=KerrOrbitalSpacetime(whatever) line and the st.orbit(whatever) line, add the line RM=st.radiusM(). (Edit: or just copy the whole program from the thread again - the bug isn't in that version *cough*.)

Note that I wrote that program in python 2. I guess you've got python 3. You may find it doesn't work, although the differences aren't huge for this kind of programming.

 

[etotheipi]

Thanks! It works, wooooo