RC circuit analysis using phasors

[VinnyCee]

Homework Statement

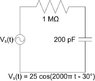
I can't post pictures as I do normally, so you'll have to deal with the cumbersome attachment method! It's just a simple RC circuit. Resistor on top, capacitor on right side with the sinusoidally varying voltage source on the left.

$$V_s(t)\,=\,25\,cos\left(2000\,\pi\,t\,-\,30^{\circ}\right)$$

Obtain an expression for $v_c(t)$, the voltage across the capacitor.

NOTE: Picture of circuit is attached.

Homework Equations

$$A\,cos\left(\omega\,t\,+\,\phi_0\right)\,\,\longrightarrow\,\,A\,e^{j\,\phi_0}$$

$$j\,=\,e^{j\,\frac{\pi}{2}}$$

Various equations and conversions from the text, Fundamentals of Applied Electromagnetics (Ulaby, 5 ed.) PROBLEM 1.21

The Attempt at a Solution

I obtained the voltage equation for the RC circuit as:

$$R\,i(t)\,+\,\frac{1}{C}\,\int\,i(t)\,dt\,=\,v_s\,(t)$$

Now, I convert to phasor form:

$$R\,\tilde{I}\,+\,\frac{1}{C}\,\left(\frac{1}{j\,\omega}\,\tilde{I}\right)\,=\,V_s$$

The book gives a conversion to get the phasor expression for the current:

$$\tilde{I}\,=\,V_0\,e^{j\,\left(\phi_0\right)}\,\frac{j\,\omega\,C}{j\,\omega\,C\,R\,+\,1}$$

I apply this formula, given for the RC circuit by the text, and I get this:

$$\tilde{I}\,=\,25\,e^{-j\,30^\circ}\,\frac{j\,\left(2000\,\pi\right)\,\left(200\,X\,10^{-12}\right)}{j\,\left(2000\,\pi\right)\,\left(200\,X\,10^{-12}\right)\,left(1\,X\,10^6\right)\,+\,1}$$

$$\tilde{I}\,=\,25\,e^{-j\,30^\circ}\,\frac{j\,4\,X\,10^{-7}\,\pi}{j\,0.4\,+\,1}$$

Then, after doing some manipulation of the complex number:

$$\tilde{I}\,=\,0.0000229\,+\,j\,0.0000180\,=\,2.29\,X\,10^{-5}\,+\,j\,1.8\,X\,10^{-5}$$

I know that this is probably not correct, but I went ahead and used it in the subsequent equation (also given in the text) to find the capacitor voltage phasor:

$$\tilde{V_c}\,=\,\frac{\tilde{I}}{j\,\omega\,C}$$

After some plug & chug…

$$\tilde{V_c}\,=\,14.3\,-\,j\,18.2$$

This is NOT the answer given in the text! I know I didn't convert back from phasor form, but still... The correct answer is:

$$V_c(t)\,=\,15.57\,cos\left(2000\,\pi\,t\,-\,81.5^{\circ}\right)$$

Where did I go wrong? Can anyone get me started on the right track here?

 

[VinnyCee]

Any ideas? This problem has been bothering me for a week or so :)

 

[tongpu]

What you want to do is express everything in impedance (Z).

Since Vs is in cosine form ... phasor of it would be 25{-30 or 25cos30 - jsin30 (if { means phasor)

Then you want Z of c and r in the circuit.. given by the equations..
Zr = R and Zc= -1/(jwc)

Since impedances are expression with units of resistance and you have a series circuit just get Zeq by summing the Zl and Zr. Then to change to phasors... Zeq = R + -1/(jwc) = some form with real and imaginary => change that to phasor...

then to get I(t) which is the same for C and R, you have I(t)=V/Zeq which gives another phasor expression..

finally, to get Vc(t) you just use I(t)Zc