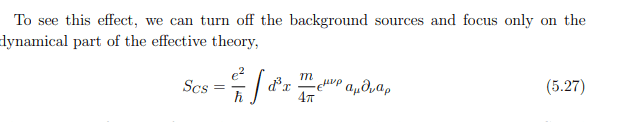SUMMARY
The discussion focuses on the process of reading canonical commutation relations from the action in the context of quantum field theory, specifically using the Lagrangian formulation. The canonical quantization method is outlined, detailing how to derive the canonical conjugate momenta from the Lagrangian, which is expressed as \(\mathcal{L} = \frac{me^{2}}{4\pi \hbar} \epsilon^{\mu\nu\rho} a_{\mu} \partial_{\nu} a_{\rho}\). The equal-time commutation relation is established as \(\big[ a_{1}(x), \pi^{1}(x') \big] = i\hbar \delta^{2}(x - x')\). References to potential pitfalls in naive applications of canonical quantization, such as with the spinning top, are also noted.
PREREQUISITES
- Understanding of canonical quantization in quantum field theory
- Familiarity with Lagrangian mechanics and field theory
- Knowledge of commutation relations and their significance in quantum mechanics
- Basic grasp of group theory and Noether's theorem
NEXT STEPS
- Study Hagen Kleinert's book on path integrals for practical examples of canonical quantization
- Explore the implications of Noether's theorem in quantum field theory
- Learn about the derivation and application of equal-time commutation relations
- Investigate the limitations and challenges of canonical quantization in non-relativistic quantum theories
USEFUL FOR
Physicists, particularly those specializing in quantum mechanics and quantum field theory, as well as students seeking to deepen their understanding of canonical quantization and its applications.