wnvl2
- 64
- 14
I use Reichenbach synchronisation. The one-way speed of light (OWSOL) in the x and y-direction is ##\frac{c}{2\epsilon}## and in the reverse direction it is for both ##\frac{c}{2(1-\epsilon)}## such that the average round trip speed of light is ##c##. For any choice of ##\epsilon## the physical laws should remain the sames as for ##\epsilon = \frac{1}{2}##.
My goal is to prove that the angle of incidence equals the angle of reflection. When using Huyghens it is obvous that I get a different result.
How can I prove ##i = r##?
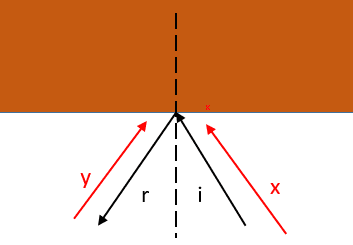
My goal is to prove that the angle of incidence equals the angle of reflection. When using Huyghens it is obvous that I get a different result.
How can I prove ##i = r##?
Last edited: