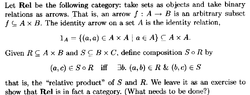Rel as a Category .... Awodey Section 1.4, Example 4, Pae 7 ....

[Math Amateur]

I am reading Steve Awodey's book: Category Theory (Second Edition) and am focused on Section 1.4 Examples of Categories ...

I need some further help in order to fully understand some aspects of the definition of the category Rel ... ...

The definition of the category Rel ... reads as follows:View attachment 8387
I am having trouble fully understanding the definition of the identity arrow ...I will use an example to illustrate my problems ...Let the category $$\text{Rel}_1$$ consist of two sets $$A, B$$ where

$$A = \{ 1, 2, 3 \}$$

$$B = \{ 3, 4 \} $$

so ... two arrows, for example, may be $$f_1 : A \to B$$ where $$f_1 = \{ (1, 3), (1, 4), (3, 4) \}$$

and $$f_2 : A \to B$$ where $$f_2 = \{ (1, 3) \}$$
Now .. consider $$f_3 : A \to A$$ where $$f_3 = \{ (1, 1) \}$$

and $$f_4 : A \to A$$ where $$f_4 = \{ (2, 2) \}$$

and $$f_5 : A \to A$$ where $$f_5 = \{ (3, 3) \}$$ ... BUT ...... according to Awodey's definition these arrows are all equal to the identity arrow of A ...... the identity arrow is meant to be unique ... ?Does this mean $$f_3 = f_4 = f_5$$ ... ? ... but why and how are they equal ...
Can someone please clarify the above ... ?

Peter

 

[steenis]

No, $1_A=\{(a,a) | a \in A \}$, that is all the pairs $(a,a)$ with $a \in A$

Thus $1_A=\{ (1,1), (2,2), (3,3) \}$

In your notation $1_A = f_3 \cup f_4 \cup f_5$

Now compute $f_1 \circ 1_A$.

 

[Math Amateur]

No, $1_A=\{(a,a) | a \in A \}$, that is all the pairs $(a,a)$ with $a \in A$

Thus $1_A=\{ (1,1), (2,2), (3,3) \}$

In your notation $1_A = f_3 \cup f_4 \cup f_5$

Now compute $f_1 \circ 1_A$.

Thanks Steenis ... that solves that one ...

Now working on the computation you mentioned..

Thanks again for the help ...

Peter

 

[Math Amateur]

No, $1_A=\{(a,a) | a \in A \}$, that is all the pairs $(a,a)$ with $a \in A$

Thus $1_A=\{ (1,1), (2,2), (3,3) \}$

In your notation $1_A = f_3 \cup f_4 \cup f_5$

Now compute $f_1 \circ 1_A$.

Hi Steenis ...You write:"... ... Now compute $f_1 \circ 1_A$ ... ... "

First ... define composition ...

If we are given two arrows $$f : A \to B$$ and $$g : B \to C$$ ...

... then ...

$$g \circ f = \{ \left \langle a, c \right \rangle \in A \times C \mid \exists \ b \ ( \left \langle a, b \right \rangle \in f \text{ and } \left \langle b, c \right \rangle \in g ) \} $$so, in particular, for $$f_1 : A \to B$$ and $$1_A : A \to A$$ we have ...

$$f_1 \circ 1_A = \{ \left \langle a, b \right \rangle \in A \times B \mid \exists \ x \ ( \left \langle a, x \right \rangle \in 1_A \text{ and } \left \langle x, b \right \rangle \in f_1 ) \}$$ ... ... ... ... ... (1)
Now ... showing informal working ... following (1) we have

$$\left \langle 1, 1 \right \rangle \in 1_A \text{ and } \left \langle 1, 3 \right \rangle \in f_1 \Longrightarrow \left \langle 1, 3 \right \rangle \in f_1 \circ 1_A $$ where $$x = 1$$$$\left \langle 1, 1 \right \rangle \in 1_A \text{ and } \left \langle 1, 4 \right \rangle \in f_1 \Longrightarrow \left \langle 1, 4 \right \rangle \in f_1 \circ 1_A$$ where $$x = 1$$$$\left \langle 3, 3 \right \rangle \in 1_A \text{ and } \left \langle 3, 4 \right \rangle \in f_1 \Longrightarrow \left \langle 3, 4 \right \rangle \in f_1 \circ 1_A$$ where $$x = 3$$Thus $$f_1 \circ 1_A = \{ \left \langle 1, 3 \right \rangle , \left \langle 1, 4 \right \rangle , \left \langle 3, 4 \right \rangle \}$$
Is the above computation correct?

Peter

 

[steenis]

Yes, correct, and why did you already expect this answer ?

 

[Math Amateur]

Yes, correct, and why did you already expect this answer ?

Hmm ... not sure that i did expect it ...

Still reflecting on this ...

Peter***EDIT***

Oh! Obvious really ... because$$ f_1 \circ 1_A = f_1$$ ...

Peter

 

[steenis]

allright, $1_A$ is an identity arrow in Rel