Discussion Overview
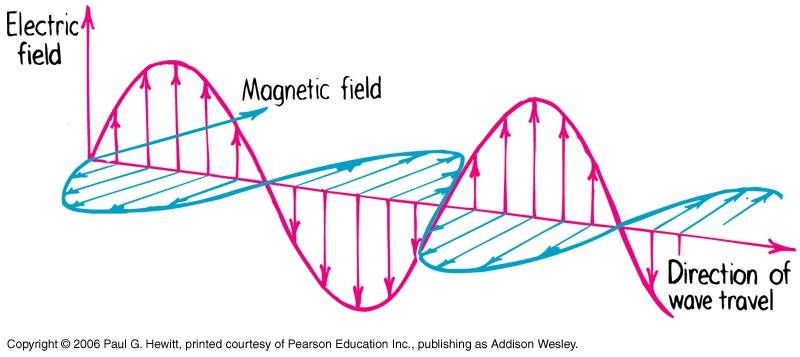
The discussion centers on the relationship between the electric field of electromagnetic waves and the probability amplitude associated with photons. It explores theoretical aspects of wave descriptions in quantum mechanics and classical electromagnetism, as well as the implications of these relationships in the context of photon behavior.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
Main Points Raised
- Some participants propose that electromagnetic waves can be described by Maxwell's equations, while photons are described by probability waves, raising questions about their relationship.
- One participant notes that intensity is proportional to the square of both the electric field amplitude and the probability amplitude.
- Several participants express that the question regarding the relationship between the electric field and probability amplitude is commonly asked, suggesting a broader interest in the topic.
- Another participant emphasizes that photons cannot be described by the non-relativistic Schrödinger equation, indicating that their quantum behavior differs from that of non-relativistic particles.
- A later reply discusses the concept of photon states being described by Fock states and the relationship of the electric field to these states through field operators.
- One participant questions the meaning of the bold p in the Schrödinger equation for photons, suggesting it may represent momentum.
Areas of Agreement / Disagreement
Participants express differing views on the relationship between the electric field and probability amplitude, with no consensus reached on whether they are directly proportional or how they relate given their different natures (vector vs. scalar).
Contextual Notes
The discussion highlights limitations in understanding the relationship due to the differing frameworks of classical electromagnetism and quantum mechanics, as well as the absence of a spatial wavefunction for photons in the traditional sense.
