Relative motion with constant acceleration

[MatinSAR]

Homework Statement

Two cars A and B are moving towards each other with speeds of 8m/s and 12m/s respectively. When the distance between the two cars is 102m, both drivers brake at the same time. If both cars decelerate with an acceleration of 1 m/s², how many seconds after the moment of braking will the two cars hit each other?

Relevant Equations

X=X0+V0t+(1/2)at^2

I think the question is wrong.
My answer :

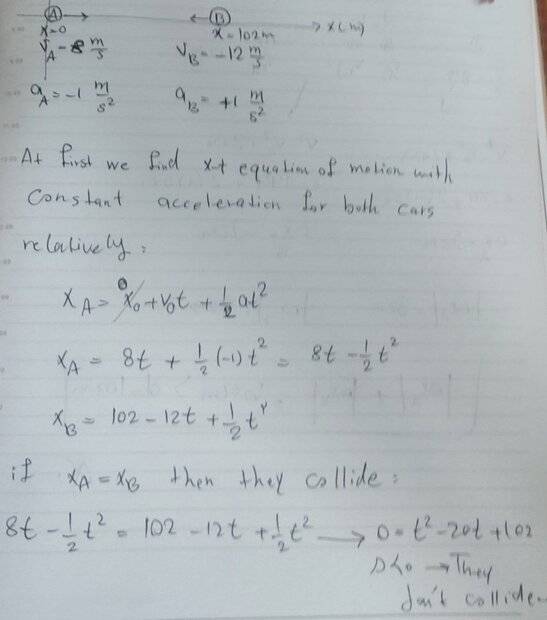
But it should be wrong because :

I think the question is wrong … But I'm not sure …

 

[Lnewqban]

The acceleration of B can’t be positive; its velocity is never increasing.

 

[haruspex]

The acceleration of B can’t be positive; its velocity is never increasing.

Slowing down means the acceleration and velocity have opposite signs, which they do.
The OP is taking the same direction as positive for all accelerations and velocities.

 

[MatinSAR]

The acceleration of B can’t be positive; its velocity is never increasing.

Slowing down means the acceleration and velocity have opposite signs, which they do.
The OP is taking the same direction as positive for all accelerations and velocities.

According to the question, the motion is decelerating.
So the sign of speed and acceleration of car A must be different. The same for B.
I observed this for both cars A and B. Could you please tell me where my mistake is ?!

 

[haruspex]

My answer :

Since they are initially at different speeds but decelerating at the same rate, they will not come to a stop at the same time. So you need to think about what happens when one car stops. You can’t assume it maintains the same acceleration.

 

[MatinSAR]

Since they are initially at different speeds but decelerating at the same rate, they will not come to a stop at the same time. So you need to think about what happens when one car stops. You can’t assume it maintains the same acceleration.

I've founded my mistake.
Thank you for your time.

 

[erobz]

I've founded my mistake.
Thank you for your time.

I like how we must stop and think\reason about this kinematic problem (not @haruspex ‘s first rodeo). I don’t think I’ve ever saw one like this. Good problem!

 

[MatinSAR]

I like how we must stop and think\reason about this kinematic problem (not @haruspex ‘s first rodeo). I don’t think I’ve ever saw one like this. Good problem!

Yes it was a good problem.

I like how we must stop and think\reason about this kinematic problem

I think the answer is 10 seconds.

 

[PeroK]

I think the answer is 10 seconds.

I think so too. The first car stops after 8 seconds, having traveled 32 metres. The second car travels 70 metres in 10 seconds.