santimirandarp
- 21
- 0
The problem
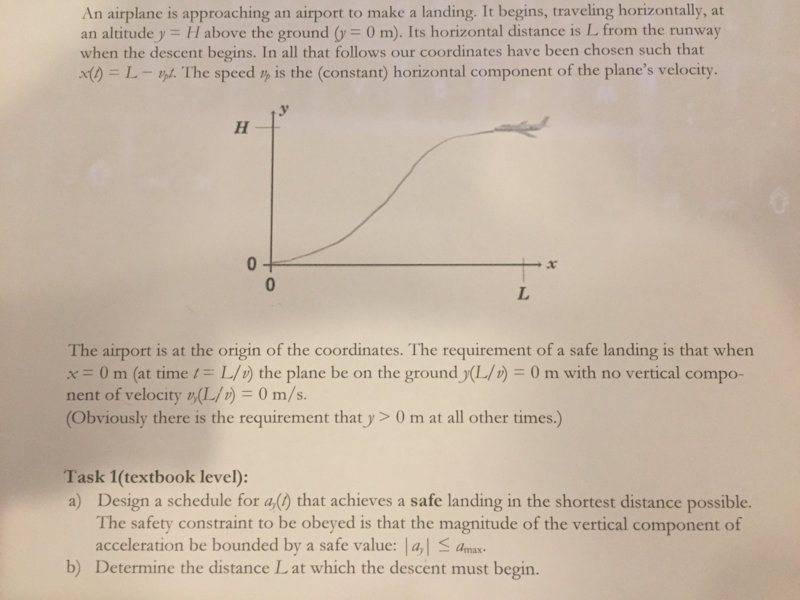
I'm pasting the problem below mainly for the plot of y vs x.
A possible way to think of it
I suppose the important thing here is to find y(t) with the condition that -amax<ay<amax, and vy(L/vp)=0
My attempt
I've modeled acceleration as a(t)=-kt and got an equation for y(t) as a function of t3 which can be replaced by L/v. But the problem is that, plotting on gnuplot, the solution doesn't convince me. Would you give me some hints on how to model a(t), please?
I'm pasting the problem below mainly for the plot of y vs x.
A possible way to think of it
I suppose the important thing here is to find y(t) with the condition that -amax<ay<amax, and vy(L/vp)=0
My attempt
I've modeled acceleration as a(t)=-kt and got an equation for y(t) as a function of t3 which can be replaced by L/v. But the problem is that, plotting on gnuplot, the solution doesn't convince me. Would you give me some hints on how to model a(t), please?
Attachments
Last edited:
