SUMMARY
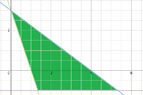
The discussion focuses on graphing the system of inequalities: $$3x + 4y \le 12$$, $$3x + y \ge 3$$, and $$y \ge -1$$. Participants clarify that the solution set is represented by the triangular region formed by the intersection of the boundaries of these inequalities. The boundaries are derived from the corresponding equations, and the solution set includes points within this region, including the boundaries due to the weak inequalities.
PREREQUISITES
- Understanding of linear inequalities and their graphical representation
- Familiarity with the concept of solution sets in the context of inequalities
- Ability to manipulate and rearrange equations to isolate variables
- Knowledge of plotting points and lines on a Cartesian coordinate system
NEXT STEPS
- Learn how to graph multiple inequalities on the same coordinate plane
- Study the method of finding intersection points of linear equations
- Explore the concept of feasible regions in linear programming
- Practice solving systems of inequalities with different boundary conditions
USEFUL FOR
Students, educators, and anyone interested in mastering graphing techniques for linear inequalities and understanding their solution sets.