SUMMARY
The discussion focuses on the mathematical process of factoring out 's' and distributing the power of 6 in the expression \(\frac{1}{2}s + \frac{1}{2}s^2\). Participants clarify that the expression can be rewritten as \(\frac{1}{2}s(1+s)\), leading to \(\left(\frac{1}{2}s + \frac{1}{2}s^2\right)^6 = \frac{1}{64}s^6(1+s)^6\). This transformation utilizes the property \((ab)^n = a^n b^n\) to simplify the expression without direct multiplication.
PREREQUISITES
- Understanding of algebraic expressions and factoring techniques
- Familiarity with the properties of exponents
- Knowledge of polynomial expressions
- Basic skills in manipulating fractions
NEXT STEPS
- Study the properties of exponents in depth, particularly \((ab)^n = a^n b^n\)
- Practice factoring polynomial expressions involving multiple terms
- Explore advanced algebraic techniques for simplifying complex expressions
- Learn about the binomial theorem and its applications in polynomial expansion
USEFUL FOR
Students studying algebra, mathematics educators, and anyone looking to enhance their skills in factoring and simplifying polynomial expressions.
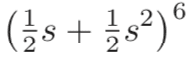 become
become
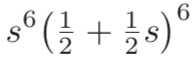 ?
?