Homework Help Overview
The discussion revolves around the process of factoring and distributing powers in algebraic expressions, specifically focusing on how to transform one bracketed expression into another while factoring out a variable and applying an exponent.
Discussion Character
- Exploratory, Mathematical reasoning, Problem interpretation
Approaches and Questions Raised
- Participants explore the steps involved in factoring an expression and distributing a power. Questions are raised about understanding the transformation without fully expanding the brackets. Some suggest clarifying the process by first factoring the expression inside the parentheses.
Discussion Status
The discussion is active, with participants providing insights on factoring techniques and the application of exponent rules. There is a collaborative effort to clarify the steps involved, though no consensus has been reached on a single method.
Contextual Notes
There is an emphasis on understanding the algebraic manipulation without resorting to multiplication of the entire expression, which may indicate a focus on conceptual understanding over procedural execution.
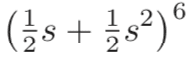 become
become
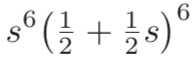 ?
?