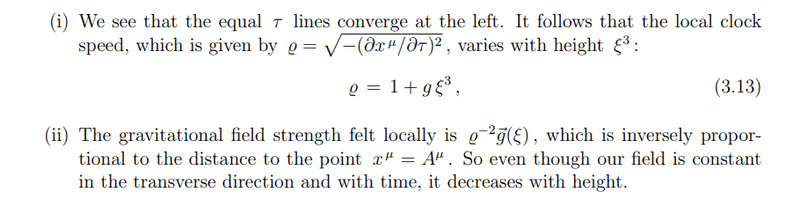SUMMARY
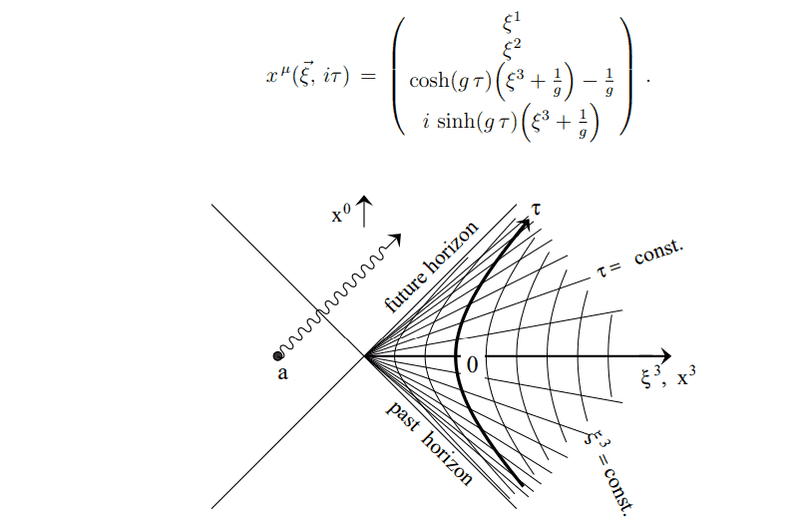
't Hooft's introduction to general relativity, specifically the derivation of the Rindler transformation, is a focal point of discussion. The formula $$\rho^{-2}g(\zeta)$$ is questioned regarding its derivation and the implications of using the ##it## convention. The text emphasizes the relationship between time dilation and gravitational potential, suggesting that the gradient of this relationship can yield the acceleration due to gravity. The discussion highlights the importance of understanding four-acceleration in Rindler coordinates for comprehending these concepts.
PREREQUISITES
- Understanding of general relativity principles
- Familiarity with Rindler coordinates
- Knowledge of four-acceleration concepts
- Basic grasp of time dilation and gravitational potential relationships
NEXT STEPS
- Study the derivation of the Rindler transformation in 't Hooft's text
- Explore the implications of the formula $$\rho^{-2}g(\zeta)$$ in general relativity
- Investigate the relationship between time dilation and gravitational potential
- Learn about four-acceleration in Rindler coordinates
USEFUL FOR
Students and researchers in theoretical physics, particularly those focusing on general relativity and its applications in understanding acceleration and gravitational effects.