kotreny
- 46
- 0
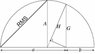
Today I was thinking about the root mean square, and I figured out a definite relationship with the Pythagorean theorem. Specifically, the root mean square of the legs of a right triangle is equal to the "average leg," i.e. the leg of a square with the hypotenuse as it's diagonal. It appears to me that this is a fairly interesting and important connection, certainly applying to distance on Cartesian coordinates and maybe explaining the usefulness of the RMS. However, when I googled it, nothing came up! I'm trying to see if this relationship has any meaning whatsoever, which I believe it should, and if so, what it means. I'm pretty sure my math isn't wrong.