gurbir_s
- 11
- 4
- TL;DR
- I am using Rosenbrock4 method from Odeint library in C++ to solve a set of differential equations. However, I see that it gives an unusual change in the result for first iteration but afterwards, gives good results. How can I solve it?
The set of equations is
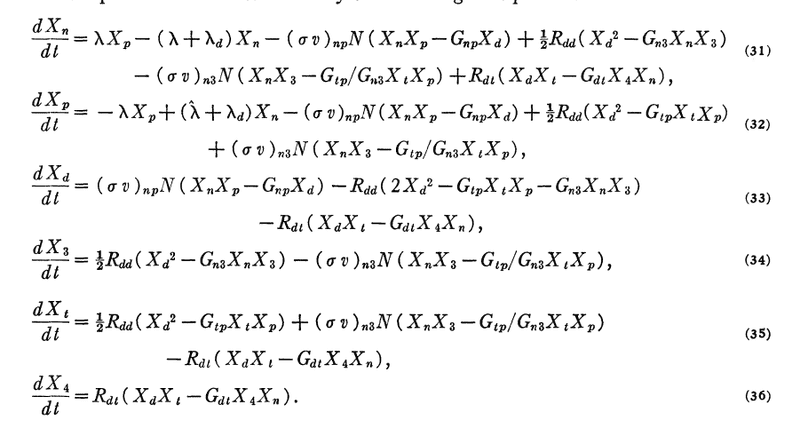
I have first tried to solve only first two equations (removing the components of other 4 equations from them.)
This is the output, where first column is the time, 2nd - X_p, and 3rd - X_n
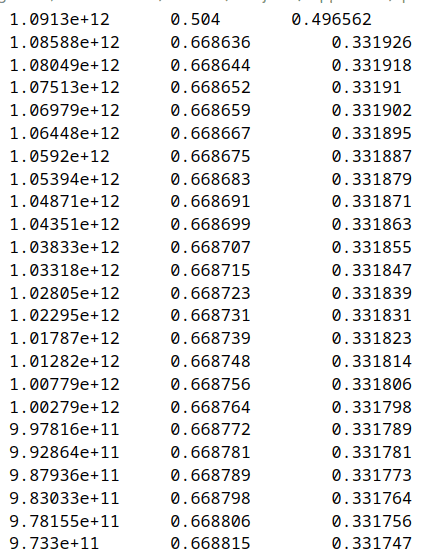
I have first tried to solve only first two equations (removing the components of other 4 equations from them.)
This is the output, where first column is the time, 2nd - X_p, and 3rd - X_n