Rotational inertia of square about axis perpendicular to its plane

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

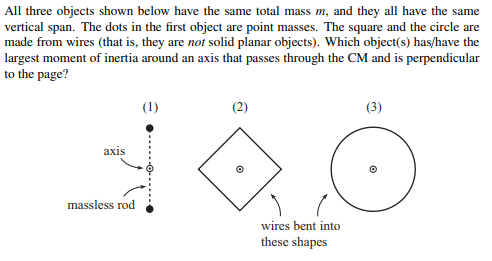
How do we calculate the moment of inertia of (2) and (3)?

For (3) I have tried,

$I_z = \int r^2 \, dm$
$ds = r$ $d\theta$
$\lambda = \frac {dm}{ds}$
$\lambda$ $ds = dm$
$\lambda r$ $d\theta = dm$
$I_z = \lambda \int r^3 d\theta$
$I_z = \lambda \int_0^{2\pi} r^3 d\theta$

EDIT:
I know how to find the moment of inertia of (3) (shown in post ##2), however, how do I find the moment of inertia of the square about z-axis?

Many thanks!

 

[Frabjous]

Look at the I_z equation and think about what it means for each of the cases. You do not need to calculate anything.

 

[member 731016]

Look at the I_z equation and think about what it means for each of the cases. You do not need to calculate anything.

Thank you for your reply @Frabjous!

I see what you mean for (3)! So
$I_z = \int r^2 dm$
$I_z = r^2 \int dm$ (since a circle has a constant radius)
$I_z = mr^2$

However, how would I find the moment of inertia of the square?

Many thanks!

 

[Frabjous]

Thank you for your reply @Frabjous!

I see what you mean for (3)! So
$I_z = \int r^2 dm$
$I_z = r^2 \int dm$ (since a circle has a constant radius)
$I_z = mr^2$

However, how would I find the moment of inertia of the square?

Many thanks!

You don’t need to. Notice that the square fits inside the circle. What does this imply?

 

[member 731016]

You don’t need to. Notice that the square fits inside the circle. What does this imply?

Thank you for your reply @Frabjous!

It implies that $I_{square} < I_{circle}$ (since mass elements are either the same radius or closer than the circle) so $I_{square} < mr^2$. However, how do we calculate the square's specific moment of inertia?

Many thanks!

 

[Frabjous]

Notice that each side of the square will have the same inertia. Take two points, like (r,0) and (0,r), and write down the equation of the line that connects them.

 

[haruspex]

$I_z = \lambda \int_0^{2\pi} r^3 d\theta$

Fwiw, you can get I_z that way. Just do the integral (trivial) then substitute for λ using m and r.

 

[member 731016]

Notice that each side of the square will have the same inertia. Take two points, like (r,0) and (0,r), and write down the equation of the line that connects them.

Thank you for your reply @Frabjous !

The equation I got was $y = -x + r$

Thank you!

 

[erobz]

Thank you for your reply @Frabjous!

It implies that $I_{square} < I_{circle}$ (since mass elements are either the same radius or closer than the circle) so $I_{square} < mr^2$. However, how do we calculate the square's specific moment of inertia?

Many thanks!

Rotate it by 90 degrees. Then just focus on the top horizontal segment. Multiply the result by 4.

 

[member 731016]

Fwiw, you can get I_z that way. Just do the integral (trivial) then substitute for λ using m and r.

Thank you for your reply @haruspex!

Sorry, how do you get $r$ in terms of $\theta$?

Thank you!

 

[haruspex]

Thank you for your reply @haruspex!

Sorry, how do you get $r$ in terms of $\theta$?

Thank you!

In (3), r is constant.

 

[member 731016]

In (3), r is constant.

Whoops thank you @haruspex! I see now :)

 

[member 731016]

Rotate it by 90 degrees. Then just focus on the top horizontal segment. Multiply the result by 4.

Thank you for your reply @erobz!

Oh ok, so maybe I use Pythagorean theorem?

Thank you!

 

[erobz]

Thank you for your reply @erobz!

Oh ok, so maybe I use Pythagorean theorem?

Thank you!

That’s the idea. You know the diagonal of the square $2r$, the rest you can figure out with that info.

 

[nasu]

You can do this without extra integrals. You can calculate the moment of inertia of one of the sides around the center by using the parallel axis theorem. You know the moment of inrtia about an axis going through the middle of the side. $I=\frac{1}{12}ma^2$ where m is the mass of one of the sides (1/4 of the total mass) and a is the side of the square. Then just add the $m(a/2)^2$ to get the moment about the center of the square (a/2 is the distance between the two centers). Once you know the moment of one side, you multiply by 4.

 

[member 731016]

Thank you both @erobz and @nasu for your replies!

I will try again with those hints, and let you know how I get on.

Thank you!

 

[member 731016]

So far @erobz and @nasu I have got

$I = \int r^2 dm$
$I = \int R^2 + x^2 dm$ Where $2R$ is the length of the diagonal which means that each side as a length $2(2)^{1/2}$
$$ I = \lambda \int_{-(2)^{1/2}R}^{(2)^{1/2}R} R^2 + x^2 dx $$
$I = \lambda R^2 + \lambda \int_{-(2)^{1/2}R}^{(2)^{1/2}R} x^2 dx$

Is everything so far correct?

Many thanks!

 

[erobz]

So far @erobz and @nasu I have got

$I = \int r^2 dm$
$I = \int R^2 + x^2 dm$ Where $2R$ is the length of the diagonal which means that each side as a length $2(2)^{1/2}$
$I = \lambda \int_{-(2)^{1/2}R}^{(2)^{1/2}R} R^2 + x^2 dx$
$I = \lambda R^2 + \lambda \int_{-(2)^{1/2}R}^{(2)^{1/2}R} x^2 dx$

Is everything so far correct?

Many thanks!

Check your algebra for $r^2$. I do not get $r^2 = R^2 + x^2$. Remember $2R$ is the squares diagonal. (that's not the only problem, but it's the first problem I see).

P.S. use the $ sign delimiters for the latex. It formats more readable with integrals and limits.

 

[member 731016]

Check your algebra for $r^2$. I do not get $r^2 = R^2 + x^2$. Remember $2R$ is the squares diagonal. (that's not the only problem, but it's the first problem I see).

P.S. use the $ sign delimiters for the latex. It formats more readable with integrals and limits.

Thank you for your reply @erobz!

Sorry, what do you mean about r?

Where R is a constant and x is a variable in the y-direction.

Many thanks?

 

[erobz]

Thank you for your reply @erobz!

Sorry, what do you mean about r?
View attachment 322246
Where R is a constant and x is a variable in the y-direction.

Many thanks?

 

[member 731016]

View attachment 322247

Thank you for your reply @erobz!

 

[nasu]

$\lambda R^2$ does not have the right dimension to be a term in the moment of inertia.

 

[member 731016]

$\lambda R^2$ does not have the right dimension to be a term in the moment of inertia.

True, thanks for pointing that out @nasu!

 

[member 731016]

$\lambda R^2$ does not have the right dimension to be a term in the moment of inertia.

Are you saying that I can't take $\lambda R^2$ out of the integral since it is a constant in the space integral?

Many thanks!

 

[member 731016]

View attachment 322247

So the new integral is so far,

$$ I = \lambda \int_{-(2)^{1/2}R}^{(2)^{1/2}R} 2R^2 + x^2 dx $$
$$ I = \frac {M}{4(2)^{1/2}R} \int_{-(2)^{1/2}R}^{(2)^{1/2}R} 2R^2 + x^2 dx $$

Many thanks!

 

[haruspex]

Are you saying that I can't take $\lambda R^2$ out of the integral since it is a constant in the space integral?

Many thanks!

You can't just take it out of the integral unchanged. How do you integrate a constant wrt x?

 

[member 731016]

You can't just take it out of the integral unchanged. How do you integrate a constant wrt x?

Thank you for your reply @haruspex! I completely forgot! Integrating $R^2$ wrt to x is $R^2x$

Thank you!

 

[erobz]

So the new integral is so far,

$$ I = \lambda \int_{-(2)^{1/2}R}^{(2)^{1/2}R} 2R^2 + x^2 dx $$
$$ I = \frac {M}{4(2)^{1/2}R} \int_{-(2)^{1/2}R}^{(2)^{1/2}R} 2R^2 + x^2 dx $$

Many thanks!

The function for square root in latex is \sqrt{} Also, I wouldn't substitute for $\lambda$ just yet, its just more symbols to juggle IMO.

 

[nasu]

So the new integral is so far,

$$ I = \lambda \int_{-(2)^{1/2}R}^{(2)^{1/2}R} (2R^2 + x^2) dx $$
$$ I = \frac {M}{4(2)^{1/2}R} \int_{-(2)^{1/2}R}^{(2)^{1/2}R}( 2R^2 + x^2 )dx $$

Many thanks!

You need to put some parantheses inside the integral. Otherwise it does not make sense.

 

[member 731016]

The function for square root in latex is \sqrt{} Also, I wouldn't substitute for $\lambda$ just yet, its just more symbols to juggle IMO.

Ok thank you @erobz , that is good advice!

 

[member 731016]

You need to put some parantheses inside the integral. Otherwise it does not make sense.

Thank you @nasu! I will do that next time, since the dx is multiped to the integrand

 

[member 731016]

I got $I = \frac {16MR^2}{3}$ I don't think is correct though since $I < MR^2$

Many thanks!

 

[haruspex]

I got $I = \frac {16MR^2}{3}$ I don't think is correct though since $I < MR^2$

Many thanks!

Not sure where all those $R\sqrt 2$ terms come from in your integral. Shouldn’t they be $R/\sqrt 2$?

 

[member 731016]

Not sure where all those $R\sqrt 2$ terms come from in your integral. Shouldn’t they be $R/\sqrt 2$?

Thank you for your reply @haruspex !

I'm not sure maybe? I got $R\sqrt 2$ from the diagram (courtesy of @erobz)

Many thanks!

 

[erobz]

Thank you for your reply @haruspex !

I'm not sure maybe? I got $R\sqrt 2$ from the diagram (courtesy of @erobz)
View attachment 322322
Many thanks!

I goofed. Should be $\frac{\sqrt{2}}{2} R$

 

[member 731016]

I goofed. Should be $\frac{\sqrt{2}}{2} R$

No worries @erobz! What was the mistake?

Many thanks!

 

[erobz]

No worries @erobz! What was the mistake?

Many thanks!

$a^2 + a^2 = R^2$

$2a^2 = R^2$

$\implies a = \frac{R}{\sqrt{2}} = \frac{\sqrt{2}}{2} R$

Just carless algebra...late at night for me.

 

[member 731016]

$x^2 + x^2 = R^2$

$2x^2 = R^2$

$\implies x = \frac{R}{\sqrt{2}} = \frac{\sqrt{2}}{2} R$

Just carless algebra...late at night for me.

No worries! We all make algebra mistakes! Thank you for your reply @erobz!

So, I'm just trying to understand how you got $y\hat j = x\hat j$. I have drawn a grey square below.

I'm trying not to use circular reasoning, but did you get $y\hat j = x\hat j$ because $\vec r$ will always form a right isosceles triangle since it is a square so $\theta = 45$?

Many thanks!

 

[haruspex]

No worries @erobz! What was the mistake?

Many thanks!

You should be able to work that out yourself. R is the distance from the centre of the square to one corner. How far is it from the centre of the square to the centre of one side? If x is a displacement along a side from its midpoint, what is the range of x?

 

[member 731016]

You should be able to work that out yourself. R is the distance from the centre of the square to one corner. How far is it from the centre of the square to the centre of one side? If x is a displacement along a side from its midpoint, what is the range of x?

Thank you for your reply @haruspex!

I was trying to consider cases where $\vec r ≠ R$ for when the position vector is pointing somewhere along to the mass element on the sides not to the corners.

When $\vec r = R$, I can see that since it square then each side of the right triangle will have equal sides of length $x$.

I think the range of x for that case would be from $0$ at the midpoint to $\frac {R}{\sqrt{2}}$ at the centre of one side.

Dose this special case hold for $\vec r ≠ R$?

Many thanks!

 

[haruspex]

Thank you for your reply @haruspex!

I was trying to consider cases where $\vec r ≠ R$ for when the position vector is pointing somewhere along to the mass element on the sides not to the corners.

When $\vec r = R$, I can see that since it square then each side of the right triangle will have equal sides of length $x$.

I think the range of x for that case would be from $0$ at the midpoint to $\frac {R}{\sqrt{2}}$ at the centre of one side.

Dose this special case hold for $\vec r ≠ R$?

Many thanks!

Why do you want to solve this using vectors? It's straightforward using scalars and the parallel axis theorem.

Edit: rereading your post, I don’t understand it. How are you defining $\vec r$ and x?

 

[erobz]

 

[erobz]

No worries! We all make algebra mistakes! Thank you for your reply @erobz!

So, I'm just trying to understand how you got $y\hat j = x\hat j$. I have drawn a grey square below.
View attachment 322331
I'm trying not to use circular reasoning, but did you get $y\hat j = x\hat j$ because $\vec r$ will always form a right isosceles triangle since it is a square so $\theta = 45$?

Many thanks!

The vector $\vec{r}$ varies, in both magnitude and direction, but for that horizontal segment It will always have the form:

$$ \vec{r} = x ~{\hat i} + \frac{\sqrt{2}}{2} R ~{\hat j}$$

 

[erobz]

So you are going to have to change the integrand to what it should be, and your limits of integration.

And to echo @haruspex, do it using @nasu approach (without integration) as a concomitant method.

 

[member 731016]

Why do you want to solve this using vectors? It's straightforward using scalars and the parallel axis theorem.

Edit: rereading your post, I don’t understand it. How are you defining $\vec r$ and x?

Thank you for your reply @haruspex !

Sorry, let me try to explain it better.

(sorry about the tilted coordinate system, the $\hat i$ axis should be horizontal and $\hat j$ axis should be vertical)

$\vec r_1 = \sqrt {x^2 + y_1^2}$ since it has a $x\hat i$ and $y_1\hat j$ component. However since $y_1 = x$ in this special case then $\vec r_1 = \sqrt {2x^2} = R$

For this other vector their y-component is not $x$

$\vec r_2 = \sqrt {x^2 + y_2^2} ≠ R$ (cannot equal R since $\vec r_2 < \vec r_1$)

$\vec r_3 = \sqrt {x^2 + y_3^2} ≠ R$

So what I was saying is that we should consider the general case where,

$\vec r = \sqrt {x^2 + y^2}$

Where x is a constant equal to $\frac {\sqrt {2}}{2}R$ and y is a variable position vector component in the y-direction.

However, if we choose a different coordinate system, such as what @erobz has done in post #43

Then now y a constant equal to $\frac {\sqrt {2}}{2}R$ and x is variable position vector component in the y-direction.

I think the confusing thing about this problem is choosing the right side to find the moment of inertia for and defining the right coordinate system. What do you think?

How would you solve this using the parallel axis theorem out of curiosity?

Many thanks!

 

[member 731016]

So you are going to have to change the integrand to what it should be, and your limits of integration.

And to echo @haruspex, do it using @nasu approach (without integration) as a concomitant method.

Thank you for your reply @erobz!

I am curious to try both approach's :)

Many thanks!

 

[member 731016]

View attachment 322339

Thank you @erobz!

I think I now understand where you get that constant from now. So basically, you assume that both sides of the triangle are equal which means that angle must be 45 degrees.

So $\sin45 = x/R$ which gives your result.

Is that how you did it?

Many thanks!

 

[member 731016]

The vector $\vec{r}$ varies, in both magnitude and direction, but for that horizontal segment It will always have the form:

$$ \vec{r} = x ~{\hat i} + \frac{\sqrt{2}}{2} R ~{\hat j}$$

Thank you for that @erobz!

 

[erobz]

Thank you @erobz!

I think I now understand where you get that constant from now. So basically, you assume that both sides of the triangle are equal which means that angle must be 45 degrees.
View attachment 322347
So $\sin45 = x/R$ which gives your result.

Is that how you did it?

Many thanks!

Yes, that will always be the case for a square.

 

[nasu]

Won't be easier to just find the moment of inertia for a square of side L and mass m and then use the results for any value of L and for any way this side is related to another parameter in the problem, like to the radius here? You can do this in two or three lines, even by using the integral.
For one side of the square, the moment of inertia relative to the center is just $$\int_{-L/2}^{L/2} [(L/2)^2+x^2]\lambda dx =\lambda L (L/2)^2+\lambda \frac{x^3}{3}\Big|_{-L/2}^{L/2} =\lambda L (L/2)^2+\lambda \frac{2L^3}{3\times 8}$$
I considered the x axis parallel to the side I am looking at.
Using $M=\lambda L$ you get
$$I_{side} =m\frac{L^2}{4}+m \frac{L^2}{12}$$
The last term is the moment of inertia for an axis going through the center of the bar (look it up in a table) and the first term is what you add by using the parallel axis theorem. You could write this right away, without any integral.
Then the monemt of the square is just $I_{square}=4I_{side}$.
Only now is time to see what happens if $L=R\sqrt{2}$.