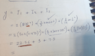SUMMARY
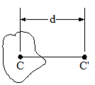
The discussion centers on calculating the rotational moment of inertia for a system involving three spheres on a pipe. Participants clarify the correct axis of rotation, debating whether it is about the x-axis or y-axis, with consensus leaning towards the x-axis due to the geometry of the setup. The Parallel Axis Theorem is highlighted as essential for accurately determining the moment of inertia, particularly for the outer spheres treated as point masses. The standard formula for the moment of inertia of a solid sphere, ##(2/5)mr^2##, is also referenced, emphasizing the need for precise application in calculations.
PREREQUISITES
- Understanding of rotational dynamics and moment of inertia
- Familiarity with the Parallel Axis Theorem
- Knowledge of the moment of inertia formulas for solid spheres and rods
- Basic geometry related to axes of rotation
NEXT STEPS
- Study the application of the Parallel Axis Theorem in various contexts
- Learn the derivation of moment of inertia formulas for different shapes
- Explore examples of rotational motion involving multiple bodies
- Practice problems involving moment of inertia calculations for complex systems
USEFUL FOR
Students preparing for physics exams, particularly those studying rotational dynamics, as well as educators seeking to clarify concepts related to moment of inertia and the Parallel Axis Theorem.