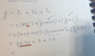- #1
SakuRERE
- 68
- 5
Homework Statement
Homework Equations
The Attempt at a Solution
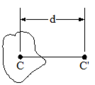
i just don't know from where to take the R which is colored with brown, in the 2(MR^2), what is the R here exactly, because i took the radius of the sphere , but i get different answer althought it's near.