mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
Let $ \tau_v: \mathbb{R}^2 \rightarrow \mathbb{R}^2, \ \ x \mapsto x + v $ be the shift by the vector $ v \in \mathbb{R}^2 $.
Let $ \sigma_a: \mathbb{R}^2 \rightarrow \mathbb{R}^2 $ be the reflection on the straight line through the origin, where $ a $ describes the angle between the straight line and the positive $ x $ axis.
One can show that the mapping $\sigma_a$ is linear.
Let $ \tau_v: \mathbb{R}^2 \rightarrow \mathbb{R}^2, \ \ x \mapsto x + v $ be the shift by the vector $ v \in \mathbb{R}^2 $.
Let $ \sigma_a: \mathbb{R}^2 \rightarrow \mathbb{R}^2 $ be the reflection on the straight line through the origin, where $ a $ describes the angle between the straight line and the positive $ x $ axis.
One can show that the mapping $\sigma_a$ is linear.
- Determine $\sigma_a\begin{pmatrix} 1\\ 0\end{pmatrix}$ and $\sigma_a\begin{pmatrix} 0\\ 1\end{pmatrix}$ by making a sketch. Determine the matrix $s_a: = M (\sigma_a)$.
- Show that
- $\tau_v\circ \tau_w=\tau_{v+w}$
- $\delta_a\circ \tau_v=\tau_{\delta_a(v)}\circ \delta_a$
- $\sigma_a\circ \sigma_a=\text{id}_{\mathbb{R}^2}$
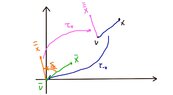
- Let's consider rotation around an arbitrary point. Let $d_{a,v}:\mathbb{R}^2\rightarrow \mathbb{R}^2, \ \ x\mapsto Ax+w$ the rotation around the angle $a$ and the pont $v$. Show at a graph that $d_{a,v}=\tau_v\circ d_a\circ \tau_{-v}$. Determine then $A\in M_2(\mathbb{R})$ and $w\in \mathbb{R}^2$ in respect to $ a$ and $ v$ .
- For $\sigma_a\begin{pmatrix} 1\\ 0\end{pmatrix}$ we do the following:
We draw an unit circle that goes through the point $(1,0)$.
$a$ is the angle between the x-axis and the line, say $g$. From that line $g$ we draw a line such that the angle between these two lines is equal to $a$. The intersection point of that line and the unit circle is the desired image point $(x,y)$.
View attachment 9540
We have a rotation around the origin by $a+a=2a$.
We calculate the coordinates of the image point using the rotation matrix \begin{equation*}\begin{pmatrix}\cos (2a) & -\sin (2a) \\ \sin (2a)& \cos (2a)\end{pmatrix}\begin{pmatrix} 1\\ 0\end{pmatrix}=\begin{pmatrix} \cos (2a)\\ \sin (2a)\end{pmatrix}\end{equation*}
For $\sigma_a\begin{pmatrix} 0\\ 1\end{pmatrix}$ do we consider the following graph:
View attachment 9541
- For the first bullet:
$$(\tau_v\circ \tau_w)(x)=\tau_v(\tau_w(x))=\tau_v(x+w)=(x+w)+v=x+(w+v)=\tau_{w+v}(x)$$
For the second bullet:
\begin{align*}&(\delta_a\circ \tau_v)(x)=\delta_a(\tau_v(x))=\delta_a(x+v)=d_a\cdot (x+v)=d_a\cdot x+d_a\cdot v \\ &(\tau_{\delta_a(v)}\circ \delta_a
)(x)=\tau_{\delta_a(v)}( \delta_a(x))=\tau_{\delta_a(v)}( d_a\cdot x)=d_a\cdot x+\delta_a(v)=d_a\cdot x+d_a\cdot v\end{align*}
For the third bullet:
\begin{align*}(\sigma_a\circ \sigma_a)(x)&=\sigma_a(\sigma_a(x))=\sigma_a\left (\begin{pmatrix}\cos (2a) & \sin (2a) \\ \sin (2a) &-\cos (2a)\end{pmatrix}x\right )=\begin{pmatrix}\cos (2a) & \sin (2a) \\ \sin (2a) &-\cos (2a)\end{pmatrix}\begin{pmatrix}\cos (2a) & \sin (2a) \\ \sin (2a) &-\cos (2a)\end{pmatrix}x \\ & =\begin{pmatrix}\cos^2 (2a)+\sin^2(2a) & \cos(2a)\sin (2a)-\sin(2a)\cos(2a) \\ \sin (2a)\cos(2a)-\cos(2a)\sin(2a) &\sin^2(2a)+\cos^2 (2a)\end{pmatrix}x=\begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}x=x\end{align*} - We translate by v to the origin to make the rotation by the origin. Then we make the rotation at the origin by the angle a. Then we translate by v such that we get the rotation around the point v by the angle a.
We have that \begin{equation*}d_{a,v}(x)=\tau_v(\delta_a(\tau_{-v}(x)))=\tau_v(\delta_a(x-v))=\tau_v(d_a\cdot (x-v))=d_a\cdot (x-v)+v=d_a x+ (I-d_a)v \end{equation*}
So we get $A=d_a$ and $w=(I-d_a)v$.
Is everything correct and complete?
Attachments
Last edited by a moderator: