shlomi123
- 8
- 0
The roulette prediction algorithm is described here: http://pingless.co.il/roulette.pdf
And I have a problem with the formula attached
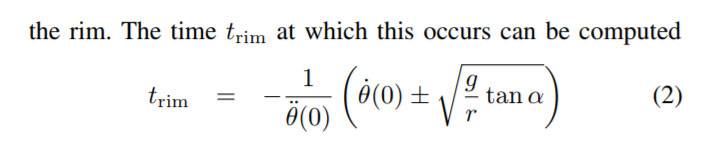
Where teta θ is position, velocity and acceleration of the ball. g is garvity force. r is the ball radius from center of the roulette. a is stator incline.
According to my calculations:
TrimCoefficient = -1/-34.13 Inch/Sec^2
ballVelocity = 120 Inch/Sec
Gravity = 386.09 Inch/Sec^2
Rrim = 14 Inches
statorIncline = (28/180)*3.14;
Trim = TrimCoefficient*(ballVelocity+math.sqrt( (Gravity/Rrim)*math.tan(statorIncline) ));
I get Trim=3.6 and it should be as I think (if you count from the start if the ball spin) Trim=18 at least.
And I have a problem with the formula attached
Where teta θ is position, velocity and acceleration of the ball. g is garvity force. r is the ball radius from center of the roulette. a is stator incline.
According to my calculations:
TrimCoefficient = -1/-34.13 Inch/Sec^2
ballVelocity = 120 Inch/Sec
Gravity = 386.09 Inch/Sec^2
Rrim = 14 Inches
statorIncline = (28/180)*3.14;
Trim = TrimCoefficient*(ballVelocity+math.sqrt( (Gravity/Rrim)*math.tan(statorIncline) ));
I get Trim=3.6 and it should be as I think (if you count from the start if the ball spin) Trim=18 at least.