Hello Roxy,
The area in question can be found with:
$$A=\int_0^1 \left|\sin(3x)-\cos(2x) \right|\,dx$$
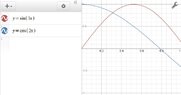
Here is a graph of the two curves over the given interval:
View attachment 2239
We need to find where the two curves intersect so that we may split the integral into two integral where the integrand of each contains the upper curve minus the lower curve. So, equating the two curves, we have:
$$\sin(3x)=\cos(2x)$$
Applying a triple-angle identity for sine on the left and a double-angle identity for cosine on the right, we have:
$$3\sin(x)-4\sin^3(x)=1-2\sin^2(x)$$
We may then arrange this as:
$$4\sin^3(x)-2\sin^2(x)-3\sin(x)+1=0$$
Factor:
$$\left(\sin(x)-1 \right)\left(4\sin^2(x)+2\sin(x)+1 \right)=0$$
The only root that results in $x$ being in the given interval comes from:
$$\sin(x)=\frac{-1+\sqrt{5}}{4}\implies x=\frac{\pi}{10}$$
And so, we may state:
$$A=\int_0^{\frac{\pi}{10}} \cos(2x)-\sin(3x)\,dx+\int_{\frac{\pi}{10}}^1 \sin(3x)-\cos(2x)\,dx$$
Applying the FTOC, we obtain:
$$A=\left[\frac{1}{2}\sin(2x)+\frac{1}{3}\cos(3x) \right]_0^{\frac{\pi}{10}}-\left[\frac{1}{3}\cos(3x)+\frac{1}{2}\sin(2x) \right]_{\frac{\pi}{10}}^1$$
$$A=\frac{1}{2}\sin\left(\frac{\pi}{5} \right)+\frac{1}{3}\cos\left(\frac{3\pi}{10} \right)-\frac{1}{3}-\frac{1}{3}\cos(3)-\frac{1}{2}\sin(2)+ \frac{1}{3}\cos\left(\frac{3\pi}{10} \right)+\frac{1}{2}\sin\left(\frac{\pi}{5} \right)$$
Combine like terms:
$$A=\sin\left(\frac{\pi}{5} \right)+\frac{2}{3}\cos\left(\frac{3\pi}{10} \right)-\frac{1}{3}-\frac{1}{3}\cos(3)-\frac{1}{2}\sin(2)$$
$$A=\frac{1}{12}\left(5\sqrt{2\left(5-\sqrt{5} \right)}-\left(6\sin(2)+4\cos(3)+4 \right) \right)\approx0.521657539274763$$