Area bounded by 3 curves: Help with Problem Solving

[MarkFL]

Here is the question:

Area between curves problem I cannot get?

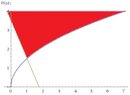
I can't get the right answer to this problem. Can someone show it to me?

It's:
Sketch the region enclosed by the curves given below. Decide whether to integrate with respect to x or y. Then find the area of the region.

The curves are

2y = 3sqrt(x)
y=4
2y + 4x = 7

I am integrating with respect to y since y=4 was given, but my webwork keeps saying my answer is wrong. Someone please help.

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Re: lilith's question at Yahoo! Anwers regarding finding the area bounded by three curves

Hello lilith,

First let's sketch the area to be found, with the bounded area shaded in red:

View attachment 1301

Now, we may integrate with respect to either $x$ or $y$. I prefer using $y$ as we may use one integral, but we will use both methods, the second as a means of checking our result.

To integrate with respect to $y$, we need to find the lower limit of integration, which is the intersection of the slant line and the parabolic curve. As we will need to know both coordinates for both methods, we will equate them to get the $x$-coordinate:

\(\displaystyle 2y=3\sqrt{x}=7-4x\)

Square both sides:

\(\displaystyle 9x=49-56x+16x^2\)

Arrange in standard quadratic form:

\(\displaystyle 16x^2-65x+49=0\)

Factor:

\(\displaystyle (x-1)(16x-49)=0\)

Discarding the extraneous root, we are left with:

\(\displaystyle x=1\,\therefore\,y=\frac{3}{2}\)

Thus, the bounded area $A$ is given by:

\(\displaystyle A=\int_{\frac{3}{2}}^4 \left(\frac{2y}{3} \right)^2-\frac{7-2y}{4}\,dy=\int_{\frac{3}{2}}^4 \frac{4}{9}y^2+\frac{1}{2}y-\frac{7}{4}\,dy\)

Applying the FTOC, we obtain:

\(\displaystyle A=\left[\frac{4}{27}y^3+\frac{1}{4}y^2-\frac{7}{4}y \right]_{\frac{3}{2}}^4=\left(\frac{256}{27}+4-7 \right)-\left(\frac{1}{2}+\frac{9}{16}-\frac{21}{8} \right)=\frac{175}{27}+\frac{25}{16}=\frac{3475}{432}\)

Now let's integrate with respect to $x$:

\(\displaystyle A=\int_{-\frac{1}{4}}^1 4-\left(\frac{7}{2}-2x \right)\,dx+\int_1^{\frac{64}{9}} 4-\left(\frac{3}{2}\sqrt{x} \right)\,dx=\int_{-\frac{1}{4}}^1 2x+\frac{1}{2}\,dx+\int_1^{\frac{64}{9}} 4-\frac{3}{2}\sqrt{x}\,dx\)

Applying the FTOC, we obtain:

\(\displaystyle A=\left[x^2+\frac{1}{2}x \right]_{-\frac{1}{4}}^1+\left[4x-x^{\frac{3}{2}}\right]_1^{\frac{64}{9}}=\left(\frac{3}{2}+\frac{1}{16} \right)+\left(\frac{256}{27}-3 \right)=\frac{25}{16}+\frac{175}{27}=\frac{3475}{432}\)