SUMMARY
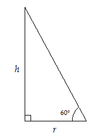
The discussion focuses on calculating the rate at which the radius of a sand pile, shaped as a right circular cone, increases 10 seconds after sand begins to fall at a rate of 9 m³ per minute. The cone has a vertical angle of 60 degrees, leading to the conclusion that the radius increases at a rate of $$3^{\frac{1}{2}}(\frac{4}{\pi})^{\frac{1}{3}}$$ meters per minute. Key steps include expressing the height in terms of the radius, differentiating the volume formula, and substituting known values to find the desired rate.
PREREQUISITES
- Understanding of calculus, specifically differentiation and the chain rule.
- Familiarity with the geometry of cones, including volume calculations.
- Knowledge of trigonometric functions, particularly tangent and their applications in geometry.
- Ability to manipulate algebraic expressions and solve for variables.
NEXT STEPS
- Study the differentiation of volume formulas for various geometric shapes.
- Learn about the application of the chain rule in related rates problems.
- Explore the relationship between volume and dimensions in conical shapes.
- Investigate practical applications of related rates in physics and engineering contexts.
USEFUL FOR
Mathematicians, physics students, engineers, and anyone interested in understanding related rates in calculus and their applications in real-world scenarios.