Sarah's question at Yahoo Answers regarding a sinusoidal function

[MarkFL]

Here is the question:

One of the largest ferris wheels ever built is in the British Airways London Eye which was completed in 2000. T?

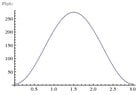
One of the largest ferris wheels ever built is in the British Airways London Eye which was completed in 2000. The diameter is 135 m and passengers get on at the bottom 4 m above the ground. The wheel rotates once every three minutes.

a) Draw a graph which represents the height of a passenger in metres as a function of time in minutes.

b) Determine the equation that expresses your height h as a function of elapsed time t

c) How high is a passenger 5 minutes after the wheel starts rotating?

d) How many seconds after the wheel starts rotating is a passenger 85 m above the ground for the first time. Answer to the nearest tenth.

10 POINTS TO BEST SOLUTIONS AND ANSWER

Here is a link to the question:

One of the largest ferris wheel ever built is in the british airways london eye which was completed in 2000. T? - Yahoo! Answers

I have posted a link there to this topic so the OP can find my response.

 

[MarkFL]

Hello Sarah,

I would do part b) first, and then plot the resulting function after that.

Since the wheel is circular and rotates at presumably a constant rate, the height of the passengers will vary sinusoidally with time. Since we are given that they are at the minimum height at time $t=0$, then we need a negative cosine function.

Since the radius of the wheel is 135 m, this will be the amplitude, and the period of the motion is said to be 3 minutes, hence we may find the angular velocity $\omega$ by:

\(\displaystyle \frac{2\pi}{\omega}=3\,\therefore\,\omega=\frac{2\pi}{3}\)

The vertical translation is the radius plus 4 metres, or 139 metres, hence the height $h$ (in metres) as a function of time $t$ (in minutes) is given by:

b) \(\displaystyle h(t)=-135\cos\left(\frac{2\pi}{3}t \right)+139\)

a) Here is a plot of the function we found for part b) over the first period:

https://www.physicsforums.com/attachments/861._xfImport

c) To find the passengers' height at time $t=5$, we need to evaluate:

\(\displaystyle h(5)=-135\cos\left(\frac{2\pi}{3}5 \right)+139=-135\left(-\frac{1}{2} \right)=\frac{413}{2}=206.5\)

d) To find when the height is 85 m for the first time, we need to equate the height to 85 m and solve for the smallest positive time:

\(\displaystyle 85=-135\cos\left(\frac{2\pi}{3}t \right)+139\)

Subtract through by 139, then multiply through by -1:

\(\displaystyle 135\cos\left(\frac{2\pi}{3}t \right)=54\)

Divide through by 135 and reduce:

\(\displaystyle \cos\left(\frac{2\pi}{3}t \right)=\frac{2}{5}\)

The inverse cosine function will give us the value we want by default.

\(\displaystyle \frac{2\pi}{3}t=\cos^{-1}\left(\frac{2}{5} \right)\)

Solve for $t$ by multiplying through by \(\displaystyle \frac{3}{2\pi}\)

\(\displaystyle t=\frac{3}{2\pi}\cos^{-1}\left(\frac{2}{5} \right)\approx0.5535151793483181\approx0.6\)

To Sarah and any other guests viewing this topic, I invite and encourage you to post other trigonometric questions here in our http://www.mathhelpboards.com/f12/ forum.

Best Regards,

Mark.

 

[SarahJeen]

Thanks Mark would you mind helping me with some other question add me on skype sunshadersg thanks sarah.

 

[MarkFL]

Hey Sarah, glad you joined MHB! (Wave)

I don't have Skype, but I will be happy to help you here in our forums. Just pick the most appropriate sub-forum for your questions, give your topics titles which indicates the nature of the question (preferably no more than two related questions per topic), and post what you have tried so far or what your thoughts are on how to begin, and I or someone else will here help guide you.(Sun)

 

[CellCoree]

Hi Sarah,

Thank you for your question about sinusoidal functions and the British Airways London Eye ferris wheel. I am happy to provide you with a response.

a) To draw a graph representing the height of a passenger in meters as a function of time in minutes, we need to first understand the characteristics of a sinusoidal function. A sinusoidal function is a function that oscillates or repeats itself at regular intervals. In this case, the ferris wheel rotates once every three minutes, so the function will repeat itself every three minutes. The height of the passenger will also change periodically as the wheel rotates. The graph will have the time in minutes on the x-axis and the height in meters on the y-axis.

b) To determine the equation that expresses the height of a passenger (h) as a function of elapsed time (t), we can use the general form of a sinusoidal function: h= A*sin(B*t+C) + D. A is the amplitude, which is half the vertical distance between the maximum and minimum values of the function. B is the frequency, which is the number of cycles per unit of time. C is the phase shift, which is the horizontal shift of the function. And D is the vertical shift, which is the mean or average value of the function. In this case, the amplitude is 65 meters (half of the diameter of 135 meters), the frequency is 1/3 (since the wheel rotates once every three minutes), the phase shift is 0 (since the wheel starts at the bottom), and the vertical shift is 4 meters (since passengers get on at 4 meters above the ground). Therefore, the equation is h= 65*sin((1/3)*t) + 4.

c) To find the height of a passenger 5 minutes after the wheel starts rotating, we can plug in t=5 into the equation we found in part b. h= 65*sin((1/3)*5) + 4 = 65*sin(5/3) + 4 ≈ 67.6 meters.

d) To find the time when a passenger is 85 meters above the ground for the first time, we can set h=85 in the equation and solve for t. 85= 65*sin((1/3)*t) + 4 → 81= 65*sin((1/3)*t) → sin((1/