- #1
serbring
- 269
- 2
Hi all,
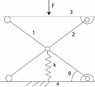
I have this mechanism and I have to calcutate the spring applied by the spring to stand the force F.
I have done a simple analysis but unfortunately it's wrong since I get the system is never in equilibrium.
http://imageshack.us/photo/my-images/651/scissor2.jpg/
Would anybody help me to understand what's wrong in what I did?
Thanks
I have this mechanism and I have to calcutate the spring applied by the spring to stand the force F.
I have done a simple analysis but unfortunately it's wrong since I get the system is never in equilibrium.
http://imageshack.us/photo/my-images/651/scissor2.jpg/
Would anybody help me to understand what's wrong in what I did?
Thanks