Static Force Analysis of Linkage

[BatsDude]

Hi!

I'm trying to complete a static force analysis on the bar linkage shown below. The goal is to find the payload mass in terms of the cylinder forces and everything else in a static environment.

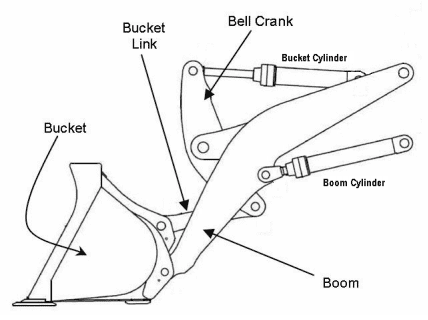
To simplify things I've made the assumption that the mass of the payload in the bucket acts at the centre of mass of the bucket. Also, the bucket cylinder is attached to the boom, and the boom is attached to an anchor point.

From what I understand, to do the static force analysis, you freeze everything in place, and then calculate the force and torque that each link must exert on each other for it to hold that position.

My attempt at the problem has been to break the linkage apart and try to work my way through each component and write down the forces and moments acting on them. For example, the bucket has a force from the boom, a force from the bucket link, and a force downwards from payload mass.

Then, I've tried to do the next component like the bucket link, and repeat the process. My attempt for the bucket and bucket link are below in the photo..

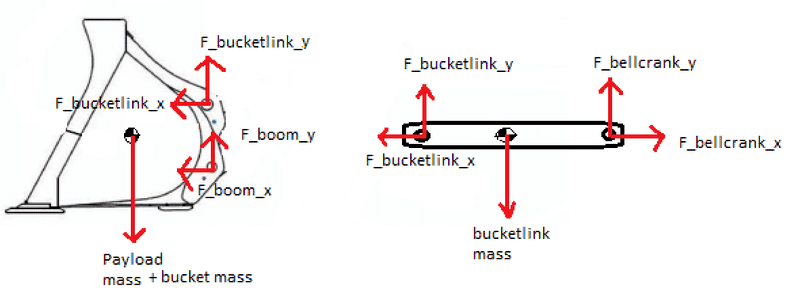
However, I'm terrible at this, so would anyone be able to help me? To reiterate, my end goal is to get an expression for the payload mass in the bucket, in terms of cylinder forces and everything else. I'm thinking the best way would be to take a sum of the torques around the boom pivot point, but I'm not really sure how to get there.

Many thanks in advance.

 

[Vigardo]

I´m not an expert on this topic, but it seems that your problem would be separated into two independent ones:

1. The force in the Bucket Cylinder to widthstand any payload acting on the center of mass (CoM) of the Bucket as a function of the position of the Boom can be determined by the law of the lever (using torques as you said). Check this: https://en.wikipedia.org/wiki/Lever
2. For a given position of the Bucket CoM, the payload can be determined by the force of the Boom Cylinder that acts on the lever arm.

This way you can compute the forces that you need in both cylinders to widthstand any given payload. Please, let me know if I´m right!

Another way to solve your problem would be performing a 2D static Finite Element Analysis using some FEA software... for example, LISA (http://www.lisa-fet.com)

Good luck, I hope this helps!

 

[Dr.D]

If you are inclined to do the necessary kinematic analysis first, this is an excellent place to apply the Principle of Virtual Work for statics. It does require, however, that you do a pretty comprehensive kinematic analysis first.

 

[BatsDude]

If you are inclined to do the necessary kinematic analysis first, this is an excellent place to apply the Principle of Virtual Work for statics. It does require, however, that you do a pretty comprehensive kinematic analysis first.

I've managed to do the kinematic analysis and every link has been defined in the global coordinate frame via vector loop analysis/ kinematic constraint equations. How would I go about the Principle of Virtual Work?

 

[Dr.D]

The system has 2DOF (two cylinders ---> 2DOF). If I were working the problem, my generalized coordinates would be the cylinder lengths. The kinematic analysis should give you the location of the load point as a function of the generalized coordinates.

Neglecting friction, the only working loads will be the cylinder forces and the bucket load (unless you want to also include component weights, which can easily be done). Write the gravitational potential energy of the system (Mgy type terms) for all the items you want to include (bucket load, member weights, etc), then write the virtual work done on the system (I have never figured out the PF Latex, so this does not work for me). The necessary expression is
deltaW = F1 delta_q1 + F2 delta_q2 - deltaV = 0
where
delta = variational operator
W = work done on the system
F1 = force in cylinder 1
F2 = force in cylinder 2
q1 = length of cylinder 1
q2 = length of cylinder 2
V = potential energy
Substituted for everything and then gather the coefficients of delta_q1 and delta_q2. Since these variations are independent, each coefficient must vanish separately. This will give you equations easily solvable for F1 and F2, the cylinder forces. With these forces in hand, you can easily solve the FBD equations for the remaining internal forces.

 

[BatsDude]

Much appreciated Dr. D. I've managed to find the cylinder forces, I'm just now struggling to make sure my FBD equations are correct.
My procedure for completing the FBD has been to separate all linkages into single components.
Then take the sum of all the forces in the Y direction = 0.
Then the sum of all the forces in X direction = 0.
Then take the moment about the centre of gravity for all the torques = 0.
So for each component, there's then 3 equations.
Is this correct? We use these equations to solve for all the unknown forces left (like payload weight in bucket)?

 

[Dr.D]

You were doing really well until you got near the end. The load in the bucket is understood to be a known value in most cases. Since it is a gravity load, it is the only reason you cannot move the cylinders with no effort at all (unless you have included the component weights).

The three equations from the FBDs will include (in some places) the cylinder forces, but you now know those which makes things much more simple. Sounds like you are almost finished! Good luck!

 

[BatsDude]

Thank you for all your help so far! I'll keep trying and will be back if I have any trouble. Many thanks once again!

 

[BatsDude]

You were doing really well until you got near the end. The load in the bucket is understood to be a known value in most cases. Since it is a gravity load, it is the only reason you cannot move the cylinders with no effort at all (unless you have included the component weights).

The three equations from the FBDs will include (in some places) the cylinder forces, but you now know those which makes things much more simple. Sounds like you are almost finished! Good luck!

Hi Dr. D. Apologies for bothering you, but I'm still slightly stuck, and I think I'm thinking about this the wrong way.
My methodology is as follows:

The cylinder forces are known.
We have 3 equations for every component in the linkage.
The unknowns in these equations are the forces that each component exert on each other, and the external force in the payload mass.
Since we know the cylinder forces, and the equations are somewhat linked, the payload mass can be solved for.

Is this correct? Many thanks and my apologies for making this difficult!

 

[Dr.D]

Presumably you had to assign the payload weight in order calculate the cylinder forces. With no payload (and no component weights), the cylinder forces should be zero.

With what you have done, you should have more equations than you need, but that is OK. Just pick what you need to complete the solution.

 

[BatsDude]

Ah, yes, this is my fault for the miscommunication. I know the pressures of the cylinders at any given time, and from that, I can calculate the force of each without having to consider the payload mass.