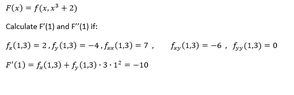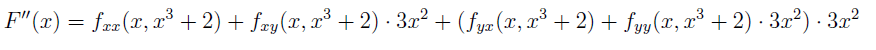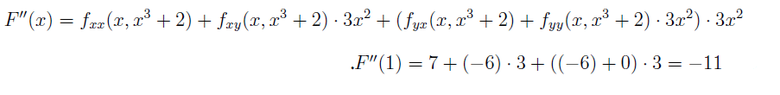Second derivative with chain rule

[Yankel]

Hello all,

I have a problem with second derivatives and chain rule.

I am working on the question attached (sorry, my Latex editor wasn't working...)

I need to find F'(1) and F''(1). I managed to solve F'(1), but I can't figure out F''(1). In the second image attached, you can see the solution I saw in the source where the question came from, but I don't understand it.

View attachment 2003

View attachment 2004

I was using a tree diagram to solve F'(1), wih f going to x and y, and y going to x.
Can you help me understand this solution ?
Thank you very much.

 

[HallsofIvy]

I think it will be better to write this as F(x)= f(u, v) with u= x, v= x^3+ 2 so that we are not using "x" and "y" to mean different things.

Then dF/dx= f_u(du/dx}+ f_v(dv/dx)= f_u+ 3x^2f_v. Yes, dF/dx(1)= f_x(1,2)(1)+ f_y(1,2)(3)= 2(1)+ (-4)(3)= 2- 12= -10.

d^2F/dx^2= (d/dx)(f_u+ 3x^2f_v)= f_uu(du/dx)+f_uv(dvdx)+ 6xf_v+ 3x^2(f_uv(du/dx)+ f_vv(dv/dx)= f_uu(1)+ f_uv(3x^2)+ 6xf_v+ 3x^2(f_uv(1)+ f_vv(3x^2)

When x= 1, u= 1 and v= 3 so this is d^2F/dx^2= 7(1)+ (-6)(3)+ 6(1)(-4)+ 3(1^2)((-6)(1)+ 0(3)= 7- 18- 24- 18= 7- 60= -53.

-

 

[Yankel]

First of all, thank you !

It took me some time to find out what you did, but I managed to create the corresponding tree diagram which puts logic into these things.

I repeated your development and final calculation and got the same result, and it even makes sense to me since I know where it came from.

Attached is the solution I had in hand. I guess they got it wrong then ?

View attachment 2007

Thanks again !