Jakub Tesar
- 2
- 0
Hi,
I am looking for the general form of 2x2 complex transformation matrix.
I have the article, that says "the relative position of a self-adjoint 2x2 matrix B with respect to A as a reference (corresponding to the transformation from the eigenspaces of A to the eigenspaces of B) is determined by two real-valued parameters."
But the general form of self-adjoint matrix is determined by four real-valued parameters (or three if I limit the matrix by the detU=1), isn't it?
I tried to start with the matrix derived from the Bloch vector, but I doubt, that it's the most general case:
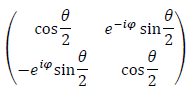
I expect I just made a mistake somewhere, but I can't find the right place.
Thank you,
Jakub
I am looking for the general form of 2x2 complex transformation matrix.
I have the article, that says "the relative position of a self-adjoint 2x2 matrix B with respect to A as a reference (corresponding to the transformation from the eigenspaces of A to the eigenspaces of B) is determined by two real-valued parameters."
But the general form of self-adjoint matrix is determined by four real-valued parameters (or three if I limit the matrix by the detU=1), isn't it?
I tried to start with the matrix derived from the Bloch vector, but I doubt, that it's the most general case:
I expect I just made a mistake somewhere, but I can't find the right place.
Thank you,
Jakub