Serial manipulator with rotational springs

[nucloxylon]

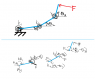
if i have a three link massless manipulator (each with length l1 l2 l3) that has rotational springs at each joint, k1 k2 k3, and I apply a force on the third link, what will be the joint angles at equilibrium?

do I find the lever arm to each joint and multiply that by the force to find the angles?

 

[jerich1000]

Is this a statics question? If so, you set up three equations, three unknowns, $$\Sigma$$X, $$\Sigma$$Y, and $$\Sigma$$M at each of the three joints.

Am I way off here? Could you provide a figure for clarification?

 

[nucloxylon]

I went back and did some fbd's. the top part of the image i attached is my problem, the second are my fbd's which now seem to indicate that the moment felt by the first link due to the force is only a short lever arm rather than a long one. is that correct?

 

[nucloxylon]

i want to make sure that the moment felt by the first link due to the force is not a big lever arm from the first joint to the location of the force on the third. (and in this way, the moment felt by the second joint would also be a longer lever arm then currently in the fbd).

I'm thinking about that because if you imagined the links to be one big bent up link, then the whole body would feel that large moment at the base. am i just confusing myself?

 

[drMS]

I went back and did some fbd's. the top part of the image i attached is my problem, the second are my fbd's which now seem to indicate that the moment felt by the first link due to the force is only a short lever arm rather than a long one. is that correct?

Hi- It is not clear to me what you mean for long/short arm.
Anyway, it seems to me that the reaction of the torsional spring k1 can be simply obtained requiring the static (is it a static structure?) equilibrium at rotation centered in the k1 point for the complete structure. In that case, as you can see, the only two involved (generalized) forces are the spring reaction and the externally applied load (F). You can also do the vertical and horizontal displacement equilibrium for the complete structure, and you have the other two reactions in (the constraint at) k1. And you can go on solving for the other substructures.

M

 

[jerich1000]

Yes, the first spring mounted to the ground joint will feel the moment created by the very end force at the tail end of the system. The problem is you can't calculate that moment trivially becasue you don't know where that end point is going to be, which is why you end up with a large system of equations and unknowns.

There are four end points, with three equations per joint. That's a 12x12 system of uknowns. A normal human being in his/her head cannot solve a 12x12 matrix. So, if your head is spinning, this is why. You need to lay out all the equations in one huge, neat, 12x12 matrix and let a calculator or computer solve it.

(I do FEA programs at work that contain a half million equations and unknowns. If I had to do that myself it would take me 200 years. And then I'd get it wrong anyway.)

 

[drMS]

Yes, the first spring mounted to the ground joint will feel the moment created by the very end force at the tail end of the system. The problem is you can't calculate that moment trivially becasue you don't know where that end point is going to be, which is why you end up with a large system of equations and unknowns.

There are four end points, with three equations per joint. That's a 12x12 system of uknowns. A normal human being in his/her head cannot solve a 12x12 matrix. So, if your head is spinning, this is why. You need to lay out all the equations in one huge, neat, 12x12 matrix and let a calculator or computer solve it.

(I do FEA programs at work that contain a half million equations and unknowns. If I had to do that myself it would take me 200 years. And then I'd get it wrong anyway.)

I clearly agreee in the case of large deflection.

 

[drMS]

Hi-
take a look to the file mathematica... It was a nice excercise..

 

[nucloxylon]

Hi- It is not clear to me what you mean for long/short arm.

Sorry, I realize I wasn't clear. Thankfully, Jerich made sense of it:

Yes, the first spring mounted to the ground joint will feel the moment created by the very end force at the tail end of the system.

Hi-
take a look to the file mathematica... It was a nice excercise..

Wow this was really amazing. I see how differently you set up the equations. I was thinking of doing something like

Tspring = Tforce

Tspring = [k1+k2 -k2 0 0; -k2 k2+k3 -k3 0; 0 -k3 k3+k4 -k4; 0 0 -k4 k4] x [theta1dot theta2dot theta3dot]'
Tforce = moment on each link = [M1 M2 M3];

where each thetadot is the difference in absolute angles (global angles i.e. to the horizontal).

In this way,
M1 = -Fx*l1*sin(theta1) + Fy*l1*cos(theta1)
M2 = -Fx*l2*sin(theta2) + Fy*l2*cos(theta2)
M3 = ...

I checked this against your formulation drMs and I'm getting the same results so that works!

I was also wondering if you had to do the reverse. Say you knew what the old angles were and you knew what the new angles were and you wanted to determine the Force that was applied. It seems to me that for a mechanism with n+ links, you would only need T2 and T3 equations to simultaneously solve for Fx and Fy. But this is assuming the force is acting on the tip of the last link.

But what if F could be applied anywhere along the mechanism? Is there some way to generalize it so that you could determine both the force and location (which link)?

In my formulation any joint above the joint with the force on it experiences zero M. So I just take the last non zero M, because that's where the force should be being applied to. I can then use another non zero M before that to simultaneously solve F, and then determine the lever arm from the last non zero M equation.

Of course if the force was applied to the first link then you'd have the Force x lever arm = M ambiguity.

 

[drMS]

I checked this against your formulation drMs and I'm getting the same results so that works!

great.

I was also wondering if you had to do the reverse. Say you knew what the old angles were and you knew what the new angles were and you wanted to determine the Force that was applied.

In the latter case you are supposing to know the equilibrium state, and you say that the force can be applied anywhere (but always perpendicular? I'll suppose so) along the mechanism.

That's an interesting point.
I would do some few considerations first.
We'll consider a mechanism with n arms with n loaded torsion spring (since a mechanism with unloaded springs at the "mechanism end" can be reduced to a lower number of arms, while unloaded springs on the middle arms simply mean that you have more than one external load) with the only load F applied (at x position) on the last arm (and perpendicular at the arm, as I suppose).
Then you can see that the solution space (theta1, theta2, ..thetaN)=func(x,F) is a mutidimensional surface, that is the solution to the problem of fixed geometry must stay on this surface. So that if the equilibrium state, the one you wish to know the loading condition (x,F), belongs to that surface, then you can get the loading condition(s), otherwise simply you need more than just one load applied to the mechanism! The fact that the solution, if it exists, may not be unique can be simply understood by thinking that the loading conditions (x=whatsoever, F=0) have all the same solution.

M