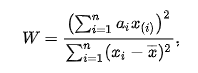SUMMARY
The discussion centers on the interpretation of the order statistic in the context of the Shapiro-Wilk test, specifically the relationship between the order statistic \(x_{(i)}\) and the original data points \(x_i\). It is confirmed that when data is sorted in ascending order, \(x_{(i)}\) equals \(x_i\). This understanding is crucial for implementing the Shapiro-Wilk test formula correctly in Python. The participants emphasize the importance of recognizing that \(x_{(i)}\) generally does not equal \(x_i\) unless the data is pre-sorted.
PREREQUISITES
- Understanding of the Shapiro-Wilk test and its application in statistical analysis.
- Familiarity with order statistics and their significance in data interpretation.
- Basic knowledge of Python programming for implementing statistical formulas.
- Ability to interpret statistical literature, such as Wikipedia entries on statistical tests.
NEXT STEPS
- Research the implementation of the Shapiro-Wilk test in Python using libraries like SciPy.
- Explore the mathematical derivation of the Shapiro-Wilk test statistic.
- Learn about other statistical tests for normality and their comparisons to the Shapiro-Wilk test.
- Study order statistics in depth, focusing on their applications in various statistical methods.
USEFUL FOR
Statisticians, data analysts, and Python developers who are implementing the Shapiro-Wilk test and require a clear understanding of order statistics in their computations.