Shear Force on Bolts mounting gearbox to engine

[Ashferico]

Homework Statement

A gearbox with mass 7.7kg is supported by bolts that are connected to an engine and pump. On the engine side, there are 4x M10 Bolts clamping the gearbox to the engine. On the pump side, there are 4x M8 Bolts clamping the gearbox to the pump. What is the shear force on each of the bolts? What is the factor of safety of the bolts? (Shear Yield Stress/Shear Stress in Bolt)

Relevant Equations

For static equilibrium:
Sum of Vertical Forces = 0
Sum of Moments around Z axis = 0
Sum of Moments around X axis = 0
Shear Force/Shear Area = Shear Stress
Shear Yield Strength/Shear Stress = Factor of Safety

Hello,

I have designed a gearbox that bolts on to a fixed engine and fixed pump. It is completely supported by them. The total mass of the gearbox and the components attaching it to the engine and pump is 7.7kg. Its centre of mass is 0.167m along the x-axis and 0.09m along the z-axis from the Fixed Engine M10 Bolts. See Figure 3 for more detail. At the engine connect there are 4 M10 Bolts and they are quite close together. At the pump connect there are 4 M8 Bolts (See Figure 2).

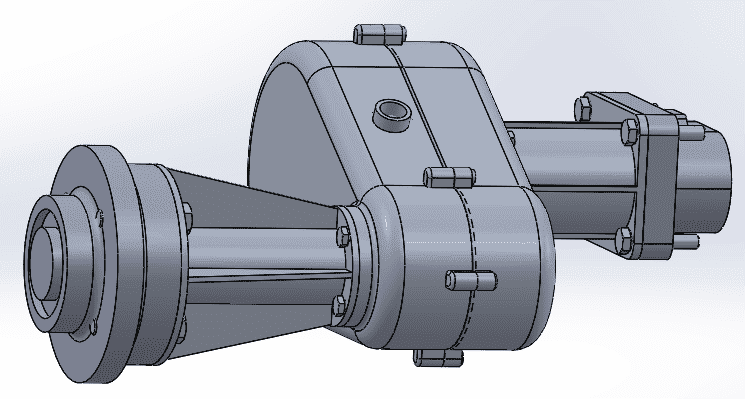
Is it accurate to reduce the gearbox to this Free Body Diagram? Each support is FIXED. Therefore it produces its own moment and reaction force. If I calculate Ra or Rb, I would have to divide them by 4 to get the shear force PER bolt.

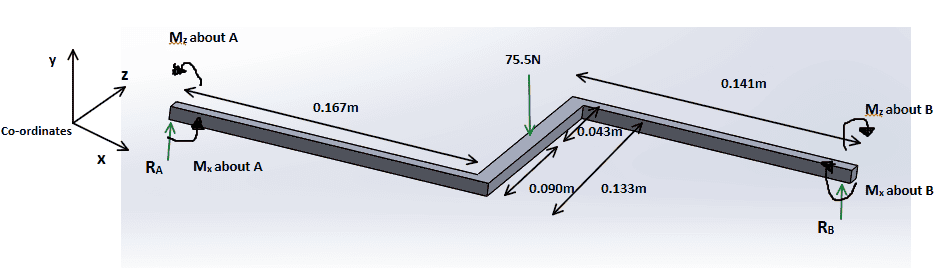
Σ Forces in Y direction = 75.5N - Ra - Rb = 0
Σ Mz about A = (0.167 x 75.5) - (0.308 x Rb) - MAZ + MBZ = 0
Σ Mx about A = (0.09 x 75.5) - (0.133 x Rb) - MAX + MBX = 0

This is where I get stuck. There are 6 unknowns. Ra, Rb, MAZ, MBZ, MAX, MBX. And only 3 equations.

Can anyone help me?

 

[haruspex]

There are 6 unknowns. Ra, Rb, MAZ, MBZ, MAX, MBX. And only 3 equations.

It's not unusual for real world systems to be "statically indeterminate".

Sometimes a unique solution can be had by taking into account the deformations that will occur. E.g. consider a four-legged table on a seemingly flat floor. If we regard the table as perfectly rigid, any three legs in contact will be stable (allow the legs to have some width), so it seems impossible to say what weight each leg bears. To solve this, we accept that the table will flex a little, so if the floor is reasonably flat and the legs near enough the same length then the loads will be close to equal.

In other situations history matters. Consider two boxes resting on a rough surface and connected by a taut string. There is a range of possible tensions in the string. E.g. it may be that the string was made taut while wet. As it dried, tension increased but not enough to overcome friction.
You will be familiar with the pattern for tightening wheel bolts to even the tensions.

In your problem, do you also need to consider acceleration? E.g. is this mounted in a vehicle?