Discussion Overview
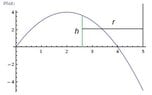
The discussion revolves around using the shell method to find the volume of the solid generated by revolving the region bounded by the curve $$y = 4x - x^2$$ and the line $$y = 0$$ about the line $$x = 5$$. Participants explore the setup of the integral and the definitions of the variables involved in the shell method.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Homework-related
Main Points Raised
- One participant states the shell method formula for volume, $$V = \int_{a}^{b} 2\pi x (f(x) - g(x))dx$$, and seeks assistance in applying it.
- Another participant introduces the concept of an arbitrary shell, defining the volume element as $$dV=2\pi rh\,dx$$ and asks for clarification on the variables $$r$$ and $$h$$.
- There is a discussion about the definitions of $$r$$ and $$h$$, with one participant suggesting that $$h$$ represents the highest point of the graph and $$r$$ is the distance from the line of revolution to the point on the curve.
- One participant provides a corrected expression for $$r$$ as $$r=5-x$$ and for $$h$$ as $$h=4x-x^2$$, leading to the formulation of the volume integral as $$V=2\pi\int_0^4 (5-x)(4x-x^2)\,dx$$.
- Another participant presents an alternative approach using a substitution $$\xi= 5 - x$$ and computes the volume integral, arriving at a numerical result of $$64\pi$$.
- One participant expresses confusion about their earlier setup of the integral and acknowledges the need to adjust their expression to match the correct formulation involving $$5-x$$.
- Another participant critiques the initial formula presented, suggesting it was intended for revolution about the $$y$$-axis and emphasizes the importance of visualizing the elemental volume directly.
- A participant claims to have arrived at an answer of $$64\pi$$, indicating a potential resolution to their inquiry.
Areas of Agreement / Disagreement
Participants express varying interpretations of the shell method and how to set up the integral correctly. There is no clear consensus on the best approach, and multiple perspectives on the definitions of the variables and the setup of the integral remain evident.
Contextual Notes
Some participants appear to be working from different interpretations of the shell method, leading to confusion regarding the appropriate setup for the integral. There are also indications that some mathematical steps may be unresolved or misapplied.