Show Triangle ABC Similarity Type Independence of B,C

[mathmari]

Hey!

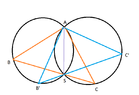
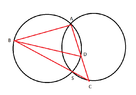
Let K,L be circles with exactly two intersection points S and A. Let $C\in L$ and $B\in K$ with $C,B\neq S,A$. I want to show the similarity type of the triangle ABC is independent of the place of B and C.

Could you explain to me what I am supposed to show?

 

[I like Serena]

Hey mathmari! (Smile)

Can you clarify what a similarity type of a triangle is?
Google doesn't seem to help.

I thought it might be the type of triangle, but whichever type we pick (equilateral. isoscales, scalene, acute, oblique, or right), we can draw circles through their corners.
And that would meet the conditions. (Thinking)

 

[mathmari]

Can you clarify what a similarity type of a triangle is?
Google doesn't seem to help.

I thought it might be the type of triangle, but whichever type we pick (equilateral. isoscales, scalene, acute, oblique, or right), we can draw circles through their corners.
And that would meet the conditions. (Thinking)

I think that it is meant that a triangle ABC is always similar to an other triangle AB'C' no matter where B or B' are on the circle K and where C or C' are on the circle L.

So, do we have to consider two such triangles ans show that they are similar? (Wondering)

 

[I like Serena]

I think that it is meant that a triangle ABC is always similar to an other triangle AB'C' no matter where B or B' are on the circle K and where C or C' are on the circle L.

So, do we have to consider two such triangles ans show that they are similar? (Wondering)

Well, if we make a drawing, I think we can immediately see that given a triangle ABC, if we pick B somewhere else, that it will not be similar. (Worried)

 

[mathmari]

Well, if we make a drawing, I think we can immediately see that given a triangle ABC, if we pick B somewhere else, that it will not be similar. (Worried)

I thought now the following:

View attachment 6988

Given that AS is fixed we have that the angle of C will be the same no matter where it is on the circle, so Angle(C)=Angle(C').
The same holds also for B, i.e., Angle(B)=Angle(B').
Since Angle(C)=Angle(C') and Angle(B)=Angle(B'), we conclude that the two triangles ABC and AB'C' have all angles the same, and they are similar.
So, we conclude that all triangles are similar no matter where B and C are.

Is this correct? (Wondering)

 

[I like Serena]

I thought now the following:

Given that AS is fixed we have that the angle of C will be the same no matter where it is on the circle, so Angle(C)=Angle(C').
The same holds also for B, i.e., Angle(B)=Angle(B').
Since Angle(C)=Angle(C') and Angle(B)=Angle(B'), we conclude that the two triangles ABC and AB'C' have all angles the same, and they are similar.
So, we conclude that all triangles are similar no matter where B and C are.

Is this correct?

Aha! So we would have the extra restriction that S must be on BC.
Let me give that a try:
\begin{tikzpicture}[ultra thick]
\def\rK{3};
\def\rL{2};
\path
(0,0) coordinate (K)
+(30:\rK) coordinate (A) node[above] {A}
+(-30:\rK) coordinate (S) node[below] {S}
+(315:\rK) coordinate (C)
+(195:\rK) coordinate (C')
(4,0) coordinate (L)
+(60:\rL) coordinate (B)
+(-60:\rL) coordinate (B')
;
\draw (K) circle (\rK) (L) circle (\rL);
\draw[orange] (A) -- (B) node[above right] {B} -- (C) node

{C} -- cycle;
\draw[cyan] (A) -- (B') node[below right] {B'} -- (C') node

{C'} -- cycle;
\end{tikzpicture}

Yep. Looks as if that would work. (Happy)

Why would the angle at C be the same as the angle at C'? (Wondering)​

 

[mathmari]

Why would the angle at C be the same as the angle at C'? (Wondering)

Isn't it because all the angles over the arc $AS$ on the circle are the same? (Wondering)

 

[I like Serena]

Isn't it because all the angles over the arc $AS$ on the circle are the same?

Ah yes, the Inscribed angle theorem.

Then it's all good! (Nod)

 

[mathmari]

Ah yes, the Inscribed angle theorem.

Then it's all good! (Nod)

(Nerd) (Yes)

If $CA$ intersects the circle $K$ at a second point $D$, how can we show that the length of $\overline{BD}$ is independent of the choice of $B$ and $C$ ? (Wondering)

Could you give me a hint? (Wondering)

 

[mathmari]

We have the following drawing:

View attachment 6990

If we consider the arc $\overline{BD}$ we have that that angle $A$ is always the same (from the first question). Do we get from that the arc must also be the same? (Wondering)

 

[I like Serena]

If $CA$ intersects the circle $K$ at a second point $D$, how can we show that the length of $\overline{BD}$ is independent of the choice of $B$ and $C$ ?

Could you give me a hint?

We have the following drawing:

If we consider the arc $\overline{BD}$ we have that that angle $A$ is always the same (from the first question). Do we get from that the arc must also be the same?

Yes. I believe so.

Since we know that the angle $A$ is always the same, it follows by applying the Inscribed angle theorem in reverse, that the chord $BD$ always has the same length. Consequently the arc $BD$ will also always have the same length. (Thinking)

 

[mathmari]

Yes. I believe so.

Since we know that the angle $A$ is always the same, it follows by applying the Inscribed angle theorem in reverse, that the chord $BD$ always has the same length. Consequently the arc $BD$ will also always have the same length. (Thinking)

I see! Thank you very much! (Sun)