DinosaurEgg
- 5
- 0
Here is the equation and my attempt on a dry-erase board:
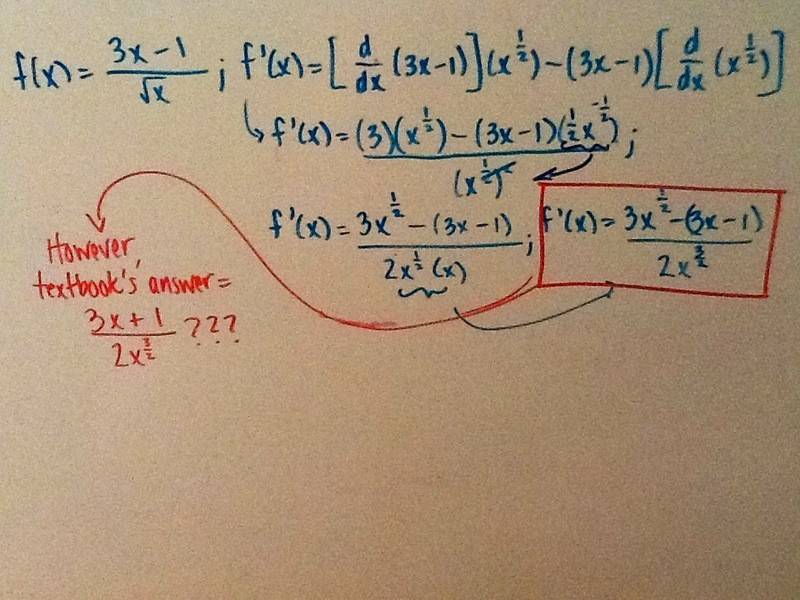
My steps are similar to the textbook's up until I hit that 3x^1/2. Why is it disappearing with their method? It's late at night and my brain is fried; I have a feeling this will be painfully obvious to me in the morning, but in case it isn't, perhaps someone can fill me in on what I missed?
My steps are similar to the textbook's up until I hit that 3x^1/2. Why is it disappearing with their method? It's late at night and my brain is fried; I have a feeling this will be painfully obvious to me in the morning, but in case it isn't, perhaps someone can fill me in on what I missed?