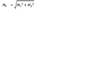SUMMARY
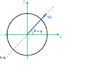
The discussion focuses on the proof of stress generated by skew bending in a circular cross section. The principle of superposition is applied, indicating that forces from torsion and bending can be simply added. The bending stress formula is established as Mf*r/I, where Mf is the moment, r is the distance from the neutral axis, and I is the moment of inertia. The maximum stress occurs at the edge of the circle, calculated as Mf*R/I, where R is the radius of the circular section.
PREREQUISITES
- Understanding of bending stress and torsion in structural mechanics
- Familiarity with the principle of superposition in mechanics
- Knowledge of moment of inertia calculations for circular cross sections
- Basic concepts of stress analysis in materials
NEXT STEPS
- Research the application of the principle of superposition in structural analysis
- Study the derivation of the moment of inertia for various cross-sectional shapes
- Explore advanced topics in torsion and bending in circular tubes
- Learn about stress distribution in non-circular cross sections
USEFUL FOR
Structural engineers, mechanical engineers, and students studying mechanics of materials will benefit from this discussion, particularly those focusing on stress analysis in circular cross sections.