Sled pulled up incline at an angle with friction

[Strawer]

Homework Statement

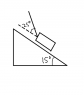
A child pulls a 3.6 kg sled at 25 degrees to a slope that is 15 degrees to the horizontal, as in the figure. The sled moves at a constant velocity when the tension is 16 N. What is the acceleration of the sled if the rope is released?

Homework Equations

F=ma, f=$\mu$N

The Attempt at a Solution

Constant velocity means that friction + the component from Fg shall equal F_Tx (tension component parallell to plane) that is F_Tx = f + F_x

Where F_Tx=cos(25)*F_T=14.5 N and F_x=3.6*9.8=9.13 N

Now I want $\mu$ so that I can calculate f. And we know that N=cos(15)*mg+T*sin(25)=40.84 N

If we go back to the start, F_Tx=$\mu$N+F_x so $\mu$= [itex]\frac{ (F_Tx-F_x) }{N}[/itex]= $\frac{14.5-9.13}{40.84}$ = 0.131

When we release the sled N will reduce to N=mg*cos(15)=34.08 and so f=0.131*34.08=4.46 N

F_res=F_x-f=9.13-4.46=4.66 N

And the acceleration is a=$\frac{F}{m}$=$\frac{4.66}{3.6}$=1.3 m/s^2

But apparently this is not correct. Could someone please tell me what I've missed, this question has been very frustrating for me :(

Also, negative signs tend to mess upp my Latex, I apologize.

 

[Strawer]

Here's the figure btw.

 

[Strawer]

Anyone?
According to the answer sheet the correct answer should be 0.67 m/s^2 but I'm starting to wonder whether that's true or not?