- #1
Student4
- 9
- 0
Stuck on really starting this one 
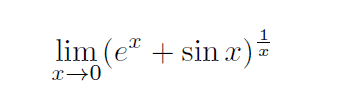relevant info: Same chapter as L’Hospital’s Rule.
Any ideas?
Any ideas?
The Small Limit Problem in L'Hospital's Rule Chapter refers to a scenario where the limit of a function approaches zero as the independent variable approaches a certain value. This can result in an indeterminate form and L'Hospital's Rule is used to find the limit in such cases.
L'Hospital's Rule states that the limit of a quotient of two functions, where both functions approach zero or infinity, can be found by taking the derivative of the numerator and denominator separately and then evaluating the limit again. This can help in solving the Small Limit Problem by converting the original indeterminate form into a determinate form.
The conditions for applying L'Hospital's Rule in the Small Limit Problem are that the limit of the quotient of the two functions must be in the form of 0/0 or ∞/∞, and both functions must be differentiable in a neighborhood around the limiting value.
No, L'Hospital's Rule can only be used to solve Small Limit Problems in which the limit of the quotient of two functions approaches 0/0 or ∞/∞. If the limit approaches a non-zero number, a different method must be used to find the limit.
Yes, there are some limitations to using L'Hospital's Rule in the Small Limit Problem. This rule can only be applied to find the limit of a quotient of two functions and cannot be used for other types of limits. Additionally, it is important to check the validity of the result obtained using L'Hospital's Rule, as it may sometimes give incorrect answers.