Jakub
- 5
- 0
Hello everyone,
I would be happy if someone explained the small reduced chi squared value to me. I have fitted a set of measured data with an exponential function, which I need for some sw calculations. The fit seams great, the origin sw also provides the reduced chi squared, but it is very small in this case. I thought it was supposed to be around 1 in the case of good fit. See the picture.
Thanks in advance for any help.
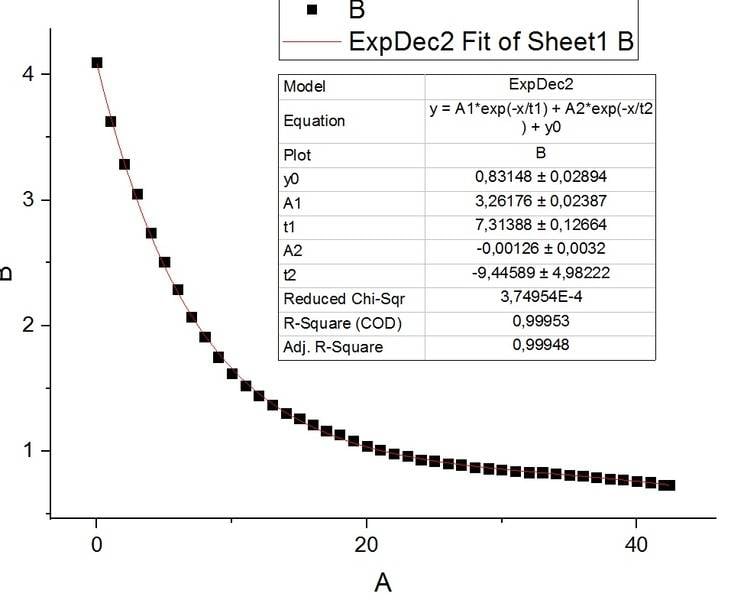
I would be happy if someone explained the small reduced chi squared value to me. I have fitted a set of measured data with an exponential function, which I need for some sw calculations. The fit seams great, the origin sw also provides the reduced chi squared, but it is very small in this case. I thought it was supposed to be around 1 in the case of good fit. See the picture.
Thanks in advance for any help.


