madsmh
- 32
- 2
Hi, as a side project I am making a solar system simulator in Python, but I am getting extreme inaccuracies.
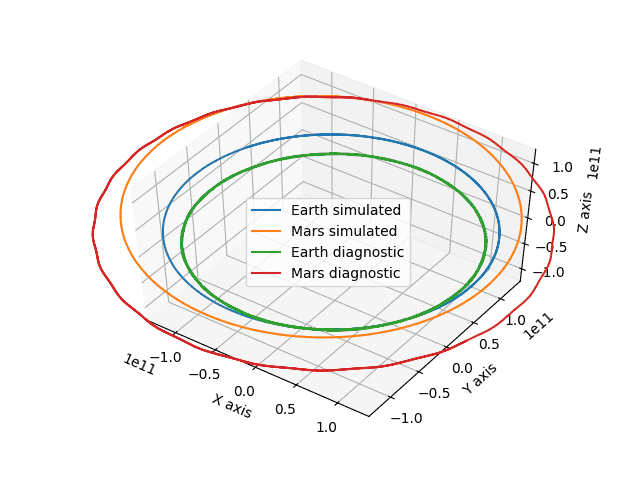
As the image shows - I am comparing the simulation to data obtained from NASA's Horizon.
I have written a a basic Verlet integrator in the Python class posten below:
And then calling the Body.step() method for each planet individially - but I am unsure whether this is the correct approach. Any advice would be welcome.
As the image shows - I am comparing the simulation to data obtained from NASA's Horizon.
I have written a a basic Verlet integrator in the Python class posten below:
Python:
import numpy as npclass Body:
"""A celestial body class, with all initial values in SI units """
def __init__(self, name, x0, y0, z0, vx0, vy0, vz0, gm, radius):
# Gravitational parameter
self.GM = gm
# Name of the body (string)
self.name = name
# Initial position of the body (m)
self.x0 = x0
self.y0 = y0
self.z0 = z0
# Position (m). Set to initial value.
self.x = self.x0
self.y = self.y0
self.z = self.z0
# Initial velocity of the body (m/s)
self.vx0 = vx0
self.vy0 = vy0
self.vz0 = vz0
# Velocity (m/s). Set to initial value.
self.vx = self.vx0
self.vy = self.vy0
self.vz = self.vz0
# Radius of the body (m)
self.radius = radius
# Storage of last integration results
self.last_coords = np.zeros(shape=(2, 3), dtype=float)
# Integration counter
self.i = 0
def compute_acceleration(self, x, y, z):
"""Computes the gravitational acceleration due to self at position (x, y) (m)"""
# Deltas
delta_x = self.x - x
delta_y = self.y - y
delta_z = self.z - z
# Deltas squared
delta_x2 = delta_x ** 2
delta_y2 = delta_y ** 2
delta_z2 = delta_z ** 2
# Acceleration in the x-direction (m/s^2)
ax = self.GM / (delta_x2 + delta_y2 + delta_z2) * \
delta_x / np.sqrt(delta_x2 + delta_y2 + delta_z2)
# Acceleration in the y-direction (m/s^2)
ay = self.GM / (delta_x2 + delta_y2 + delta_z2) * \
delta_y / np.sqrt(delta_x2 + delta_y2 + delta_z2)
# Acceleration in the z-direction (ms/s^2)
az = self.GM / (delta_x2 + delta_y2 + delta_z2) * \
delta_z / np.sqrt(delta_x2 + delta_y2 + delta_z2)
return np.array([ax, ay, az])
def step(self, dt, targets):
"""Verlet integrator"""
# dt squared
dt2 = dt ** 2
x0 = np.array([self.x0, self.y0, self.z0])
v0 = np.array([self.vx0, self.vy0, self.vz0])
if self.i == 0:
self.x = x0[0]
self.y = x0[1]
self.z = x0[2]
self.last_coords[0][:] = x0
elif self.i == 1:
a = np.zeros(shape=3, dtype=float)
for o in targets:
a += o.compute_acceleration(x0[0], x0[1], x0[2])
x1 = x0 + v0 * dt + 0.5 * dt2 * a
self.x = x1[0]
self.y = x1[1]
self.z = x1[2]
self.last_coords[1][:] = x1
elif (self.i % 2) == 0:
xnminusone = self.last_coords[0][:]
xn = self.last_coords[1][:]
a = np.zeros(shape=3, dtype=float)
for o in targets:
a += o.compute_acceleration(xn[0], xn[1], xn[2])
xnplusone = 2 * xn - xnminusone + dt2 * a
self.x = xnplusone[0]
self.y = xnplusone[1]
self.z = xnplusone[2]
self.last_coords[0][:] = xnplusone
elif (self.i % 2) != 0:
xnminusone = self.last_coords[1][:]
xn = self.last_coords[0][:]
a = np.zeros(shape=3, dtype=float)
for o in targets:
a += o.compute_acceleration(xn[0], xn[1], xn[2])
xnplusone = 2 * xn - xnminusone + dt2 * a
self.x = xnplusone[0]
self.y = xnplusone[1]
self.z = xnplusone[2]
self.last_coords[1][:] = xnplusone
self.i += 1And then calling the Body.step() method for each planet individially - but I am unsure whether this is the correct approach. Any advice would be welcome.