kazi
- 2
- 0
Hi everyone,
I have a 100 mm long, solid cylinder (shaft) with a diameter of 20 mm. The base circular surface at one end is fixed and the other end gets a torque of 100Nm.
The SolidWorks simulator (URES) results show that the diameter of this shaft increases by about 0.1 mm due to the applied torque. Similar is the outcome using Autodesk Inventor simulation. My cylinder becomes somewhat conic-like in shape, also not completely simmetrical along its original axis. So far I have only seen books with theories that begin with the assumption that the shaft cross section does not change in diameter.
Could these results be false? Can you people tell me how to get the same results on paper? Name a book that explains these results?
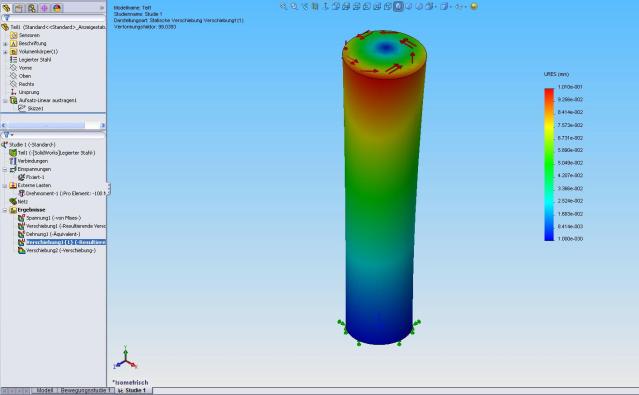
I have a 100 mm long, solid cylinder (shaft) with a diameter of 20 mm. The base circular surface at one end is fixed and the other end gets a torque of 100Nm.
The SolidWorks simulator (URES) results show that the diameter of this shaft increases by about 0.1 mm due to the applied torque. Similar is the outcome using Autodesk Inventor simulation. My cylinder becomes somewhat conic-like in shape, also not completely simmetrical along its original axis. So far I have only seen books with theories that begin with the assumption that the shaft cross section does not change in diameter.
Could these results be false? Can you people tell me how to get the same results on paper? Name a book that explains these results?
Last edited: