Discussion Overview
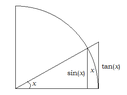
The discussion revolves around evaluating the limit $$\lim_{x\rightarrow\frac{\pi}{2}}\frac{\cos{x}}{x-\frac{\pi}{2}}$$. Participants explore various approaches to solve this limit, including substitutions and the application of trigonometric identities. The scope includes mathematical reasoning and limit evaluation techniques.
Discussion Character
- Mathematical reasoning
- Exploratory
Main Points Raised
- One participant initially attempts to convert $$\cos x$$ to $$\frac{\tan{x}}{\sin{x}}$$ but questions the applicability of this approach.
- Another participant suggests a substitution $$u=\frac{\pi}{2}-x$$ to reformulate the limit.
- Following the substitution, a participant expresses the limit as $$\lim_{u\rightarrow0}\frac{\cos{(\frac{\pi}{2}-u)}}{-u}$$.
- There is a discussion about factoring the negative sign in the denominator and applying a co-function identity to the numerator.
- Concerns are raised about encountering the indeterminate form $$\frac{0}{0}$$ in the limit expression involving $$\cos{\frac{\pi}{2}}$$.
- Another participant recalls the co-function identity $$\cos\left(\frac{\pi}{2}-\theta\right)=\sin(\theta)$$ and reformulates the limit as $$L=-\lim_{u\to0}\left(\frac{\sin(u)}{u}\right)$$.
- There is acknowledgment of the indeterminate form and reference to the well-known limit $$\lim_{x\to0}\left(\frac{\sin(x)}{x}\right)=1$$.
- A participant introduces a geometric argument using the unit circle to establish bounds for $$\frac{\sin(x)}{x}$$ and applies the squeeze theorem to conclude that $$\lim_{x\to0}\left(\frac{\sin(x)}{x}\right)=1$$.
Areas of Agreement / Disagreement
Participants express various approaches and reasoning, but there is no consensus on a final solution or method for evaluating the limit. The discussion remains exploratory with multiple perspectives presented.
Contextual Notes
Some participants note the presence of indeterminate forms and the reliance on specific limit results, which may depend on prior knowledge or assumptions about trigonometric limits.
