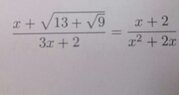Solve equation with square roots

  • Context: MHB 
  • Thread starter Thread starter theakdad
  • Start date Start date
  • Tags Tags
    Roots Square
Click For Summary

Discussion Overview

The discussion revolves around solving an equation involving square roots and fractions. Participants seek guidance on how to find all possible solutions for a specific mathematical expression, with a focus on simplifying the equation and removing fractions.

Discussion Character

  • Homework-related
  • Mathematical reasoning
  • Exploratory

Main Points Raised

  • Some participants ask for step-by-step guidance on removing fractions and finding solutions for the variable X.
  • One participant suggests starting by simplifying the square roots present in the equation.
  • Another participant proposes that the equation could be expressed as x^3 + 3x^2 = 4.
  • There is a discussion about the potential solutions, with one participant asserting that there may only be one solution.
  • Another participant expresses a desire to understand the mathematical process for proving the solution, indicating uncertainty about how to "disassemble" the expression.
  • One participant notes that while x=1, 2, -2 are suspected solutions, they emphasize the importance of verifying these solutions, mentioning that x=2 and -2 are not valid roots.

Areas of Agreement / Disagreement

Participants express various viewpoints on the potential solutions and methods for solving the equation, with no consensus reached on the correct approach or final solutions.

Contextual Notes

Participants have not fully clarified their assumptions or the specific form of the equation they are working with, leading to some ambiguity in the discussion.

theakdad
Messages
210
Reaction score
0
Can someone show me step by step guide,how to find all possible solutions for example?
 

Attachments

  • uploadfromtaptalk1381483136800.jpg
    uploadfromtaptalk1381483136800.jpg
    32.3 KB · Views: 88
Mathematics news on Phys.org
andreask said:
Can someone show me step by step guide,how to find all possible solutions for example?
Hi Andreas, and welcome to MHB. You do not say what you have tried in order to tackle this problem. I suggest that you start by looking at those square roots. Can you simplify them at all?
 
Thanks for welcome! I need to remove fractions,and get possible solutions for X. I don't know how to remove fractions,step by step would be very useful.
 
Is the solution x^3+3x^2=4?
 
Hello,
nfmja0.jpg


Regards,
$$|\pi\rangle$$
 
Thanks Petrus, can you continue?
 
Or someone else? Its urgent. Thanks.
 
Hello,
I Will post how to solve it after you post what you think you should do! Tips Dont do the homework in the last minutes

Regards,
$$|\pi\rangle$$
 
Expression skould be without fractions,and then i have to find possible solution(s) for X.
 
  • #10
andreask said:
Is the solution x^3+3x^2=4?
Hello,
My bad did not see this but that is correct! So what is x equal to?

Regards,
$$|\pi\rangle$$
 
  • #11
I think it can be only one! True?
 
  • #12
I want to know how do i get solution in math way. I can see that is 1,but how do i prove it? Can i "disassemble" my last expression? Or if you have time,show me please how would you do it! And many thanks,and sorry for my English!
 
  • #13
Hello,
$$x^2(x+3)=4$$ and you suspect that $$x=1,2,-2$$ BUT you always check if they are correct and Then you see that $$x=2,-2$$ is a fake root!

Regards,
$$|\pi\rangle$$
 
Last edited:

Similar threads

Undergrad Trouble Solving an Equation that has square roots on both sides
  • · Replies 1 ·
Replies
1
Views
2K
High School Determine a fractional square root without calculator
  • · Replies 15 ·
Replies
15
Views
2K
Undergrad Integer Square Roots of P{0,1,2,4,5,6,7,8,9}
  • · Replies 23 ·
Replies
23
Views
2K
MHB Can Cubic Roots and Square Roots Combine to Equal One?
  • · Replies 5 ·
Replies
5
Views
2K
High School Complete the square, yes, but what does it mean?
  • · Replies 19 ·
Replies
19
Views
3K
High School Why Must the Expression Inside a Square Root Be Non-Negative?
  • · Replies 16 ·
Replies
16
Views
2K
MHB How to Solve the Radical Equation Using Fifth Root and Square Root?
  • · Replies 3 ·
Replies
3
Views
2K
High School Can Higher Degree Nested Radicals Be Simplified?
  • · Replies 41 ·
2
Replies
41
Views
6K
MHB Not a "help need" but a question about "a self made square root formula"
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Calculating the root of a number by hand
  • · Replies 6 ·
Replies
6
Views
2K