MHB Solve Optimization Problem: Minimize Cost of New Highway

[thedude23]

Now I hate optimization problems and I cannot figure this one out at all.

1)

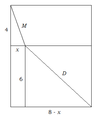
A city wants to build a new section of highway to link an
existing bridge with an existing highway interchange, which
lies 8 miles to the east and 10 miles to the south of the bridge.
The first 4 miles south of the bridge is marshland. Assume
that the highway costs 5 million per mile over marsh and 2 million per mile over dry land. The highway will be built
in a straight line from the bridge to the edge of the marsh,
then in a straight line to the existing interchange.

a)

At what point should the highway emerge from the marsh in order to
minimize the total cost of the new highway? How much is
saved over building the new highway in a straight line from the
bridge to the interchange?

b)
Just after construction has begun on the highway, the cost per km over marshland is reestimated
at $6 million per km. Find the point on the marsh/dryland boundary that would
minimize the total cost of the highway with the new cost estimate. How much would be saved
over continuing with the planned route?

My try:
Find the two triangles:

So 8 miles east and 4 miles south for the marsh.

8-x east and 6 miles south or the dryland.

So:
C(x)= (√(8^2-4^2))(5000000) + 2000000(√((8-x)^2-(6)^2))

Im pretty sure I am doing this wrong.

 

[MarkFL]

I would begin with a diagram:

View attachment 4972

Also, let's let the cost function $C(x)$ be in millions of dollars. In the diagram $M$ is the distance across marshland, and $D$ is the distance across dry land. Using the Pythagorean theorem, we then find:

$$C(x)=5\sqrt{x^2+4^2}+2\sqrt{(8-x)^2+6^2}$$

So, now you want to equate $C'(x)$ to zero and solve for $x$...what do you find?

 

[MarkFL]

Performing the differentiation and equating the result to zero, we obtain:

$$C'(x)=\frac{5x}{\sqrt{x^2+16}}+\frac{2(x-8)}{\sqrt{(x-8)^2+36)}}=0$$

Observing that for all real $x$, we have:

$$0<x^2+16$$ and $$0<(x-8)^2+36$$

we may then multiply through by $$\sqrt{\left(x^2+16\right)\left((x-8)^2+36\right)}$$ to obtain:

$$5x\sqrt{(x-8)^2+36}+2(x-8)\sqrt{x^2+16}=0$$

which we may arrange as:

$$5x\sqrt{(x-8)^2+36}=2(8-x)\sqrt{x^2+16}$$

Square both sides (and keep in mind in doing so we may introduce extraneous solutions):

$$25x^2\left((x-8)^2+36\right)=4(x-8)^2\left(x^2+16\right)$$

Distribute:

$$25\left(x(x-8)\right)^2+900x^2=4\left(x(x-8)\right)^2+64(x-8)^2$$

Arrange as:

$$21\left(x(x-8)\right)^2+900x^2=64(x-8)^2$$

Square binomials:

$$21x^2\left(x^2-16x+64\right)+900x^2=64\left(x^2-16x+64\right)$$

Distribute:

$$21x^4-336x^3+1344x^2+900x^2=64x^2-1024x+4096$$

Arrange quartic polynomial in standard form:

$$21x^4-336x^3+2180x^2+1024x-4096=0$$

Using a numeric root finder (and discarding complex and negative roots), we obtain:

$$x\approx1.25290753523819$$

To ensure this is not an approximation of an extraneous root, we should check it:

$$f(x)\equiv5x\sqrt{(x-8)^2+36}\implies f(1.25290753523819)\approx56.5626548992099$$

$$g(x)\equiv2(8-x)\sqrt{x^2+16}\implies g(1.25290753523819)\approx56.5626548992098$$

This approximation checks out. Now we need to show that this critical value minimizes the cost function. Using the first derivative test, we find:

$$C'(1)=\frac{5}{\sqrt{17}}+\frac{2(-7)}{\sqrt{85}}=\frac{5\sqrt{5}-14}{\sqrt{85}}<0$$

$$C'(2)=\frac{5}{\sqrt{5}}+\frac{2(-6)}{6\sqrt{2)}}=\frac{5\sqrt{2}-2\sqrt{5}}{\sqrt{10}}>0$$

Thus, we know the critical value is at a minimum.

Now to find the savings realized by using this value of $x$ rather than using a direct route between the two points, we first need to find the value of $x$ in this scenario, and we can use similarity to do so:

$$\frac{4}{x}=\frac{6}{8-x}\implies x=\frac{16}{5}$$

And so the savings $S$ (recall this is in millions of dollars) is found by:

$$S\approx C\left(\frac{16}{5}\right)-C(1.25290753523819)\approx1.963789989453947427$$

And so the savings to the nearest penny is: \$1,963,789.99.

I will leave it to the reader to try part b). :D