PauloBuzon
- 6
- 0
hey my fellow ME please help me with this problem I am stuck at.
1. Homework Statement
An Otto engine has a clearance volume of 7%. It produces 300 kW of power. What is the amount of heat rejected in kW?
Wnet=Qadded-Qrejected
(v2=Vc)Clearance Volume = (c)Clearance% x (Vd)Volume Displacement (v1-v2)
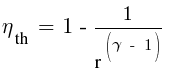 where r is the compression ratio
where r is the compression ratio
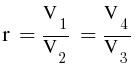
rk(compression ratio) = (c+1)/c stuck i don't know where to start
then i should be able to solve the problem where Qrejected = Qadded - Work
1. Homework Statement
An Otto engine has a clearance volume of 7%. It produces 300 kW of power. What is the amount of heat rejected in kW?
Homework Equations
Wnet=Qadded-Qrejected
(v2=Vc)Clearance Volume = (c)Clearance% x (Vd)Volume Displacement (v1-v2)
The Attempt at a Solution
rk(compression ratio) = (c+1)/c stuck i don't know where to start
then i should be able to solve the problem where Qrejected = Qadded - Work
Last edited: