Zashmar
- 48
- 0
Hi everyone please help me with this homework question!
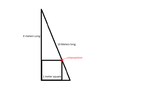
i need to solve for the left hand side of the tiangle, i hope the image uploaded succesfully i have been having trouble lately though :/
(Headbang)View attachment 635Yep if any clarrification is needed please reply and i will sort it out
Thanks
i need to solve for the left hand side of the tiangle, i hope the image uploaded succesfully i have been having trouble lately though :/
(Headbang)View attachment 635Yep if any clarrification is needed please reply and i will sort it out
Thanks