- #1
Redinorun
- 18
- 0
Hello, I would need some help with drawing these 3 triangles which are part of my homework.
Would be nice if you could just help me to at least start drawing (what to do first) the right way. Thanks.
1) Regular triangle:
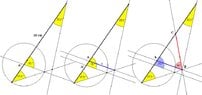
b - a = 3cm
c = 6cm
γ = 120°
2) Regular triangle:
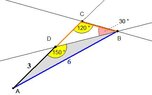
a + b + c = 16cm
\alpha = 75°
β = 60°
3) Isosceles triangle:
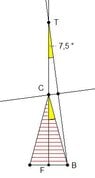
a + h = 8cm
γ = 30° (I found out that on hand of that we know that \alpha = β = 75°)
Would be nice if you could just help me to at least start drawing (what to do first) the right way. Thanks.
1) Regular triangle:
b - a = 3cm
c = 6cm
γ = 120°
2) Regular triangle:
a + b + c = 16cm
\alpha = 75°
β = 60°
3) Isosceles triangle:
a + h = 8cm
γ = 30° (I found out that on hand of that we know that \alpha = β = 75°)